O potencial gravitacional $\phi$ de uma partícula de massa $M$ num ponto situado a uma distância $x$ da partícula é
$\phi(x) = -G M/{\vert x\vert}$, onde $G$ é a constante gravitacional universal e $M$ é a massa da nossa partícula.
Daqui para frente nós vamos assumir que $G = 1$.
Dado um sistema de partículas posicionadas nos pontos $(x_i)_{i=0}^N$ o potencial gravitacional gerado por esse sistema de $N$ partículas é dado por
$\phi(x) = -\sum_{i=1}^N \frac{m_i}{\vert x - x_i\vert}.$
O mesmo vale para uma distribuição contínua de matéria,
e nesse caso o potential gravitacional vira $\phi(x) = \int_B \frac{dm(y)}{\vert y - x\vert} = \int_B dy \frac{\rho(y)}{\vert y - x\vert},$ onde $\rho(y)$ é função de densidade da distribuição de massa no corpo $B$.
Nessa última equação nós estamos supondo que $x,y$ são vetores bi-,tri-dimensionais etc. e que $dy$ é uma forma de volume, ou elemento de volume.
Vale a pena ressaltar aqui que o potential gravitacional em qualquer dos casos acima satisfaz a chamada equação de Poisson,
$$\triangle \phi = \rho(x),$$
onde $\triangle = \frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2} + \frac{\partial^2}{\partial z^2}$ é o operador de Laplace. Por quê? Consulte o seu livro favorito de mecânica clássica.
Portanto dada uma distribuição de massa $\rho(x)$ nós podemos tentar resolver para $\phi(x)$ para determinar o potencial gravitacional definido pelo corpo $B$. Pela mesma razão, o operador $\triangle$ aparece em eletromagnetismo clássico na determinação do potential elétrico definido por uma distribuição de cargas $\rho(x)$.
No caso de uma massa puntual, a densidade é uma função delta e $\rho(x) = \delta(x - x_0)$ onde $x_0$ é a localização da massa, ou carga no espaço.
A solução da equação de Laplace é para uma massa ou carga puntual é chamada de função de Green ou função de influência da carga em $x_0$.
No caso do operador de Laplace essa função de Green é exatamente o potencial gravitacional de uma partícula massiva ou carga puntual e é dada (módulo constantes de proporcionalidade) por $\phi(x) = \frac{1}{\vert x - x_0\vert}$.
Note que para uma distribuição de carga, ou de massa, contínua o potencial gravitacional é a convolução da função de Green com a distribuição de massa $\rho(x)$.
Vamos considerar agora as soluções da equação de Laplace no plano.
Isto é, em seguida nós vamos estudar a equação
$$u_{xx} + u_{yy} = 0,$$ ou ainda
$$(\frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2})u = 0.$$
Nós veremos em breve que existe uma relação profunda entre teoria potencial (soluções da equação de Laplace) e teoria de funções no plano complexo $\mathbb{C}$.
Para começar vamos recordar alguma notação do curso de cálculo complexo. Seja $z = x + \sqrt{-1}y$ onde $\sqrt{-1} = i$ é a constante imaginária.
No plano complexo $\mathbb{C}$ nós podemos definir dois operadores lineares,
$$\frac{\partial}{\partial z} = \frac{1}{2}(\frac{\partial}{\partial x} - i \frac{\partial}{\partial y} ),$$ e
$$\frac{\partial}{\partial \bar{z}} = \frac{1}{2}(\frac{\partial}{\partial x} + i \frac{\partial}{\partial y} ).$$
Nós dizemos que $f(z,\bar{z}) = u(x,y) + \sqrt{-1} v(x,y)$, diferenciável, é analítica (complexa) num aberto $U$ se
$\frac{\partial}{\partial \bar{z}} f(z,\bar{z})=0$ em $U$. Isso significa que $f = f(z)$ somente e que $f(z)$ (corolário) pode ser expandida como uma série de Taylor infinita em $z$ no aberto $U$. O aberto $U$ pode ser uma vizinhança (bola) de algum ponto $z_0$ fixo.
Funções analíticas complexas são também chamadas de holomorfas.
As partes real e imaginária da equação $\frac{\partial}{\partial \bar{z}} f(z,\bar{z})=0$ são exatamente as equações de Cauchy-Riemann do cálculo complexo:
$\frac{1}{2}(\frac{\partial}{\partial x} + i \frac{\partial}{\partial y} ) (u(x,y) + i v(x,y)) = 0 $
$\Rightarrow u_x - v_y = 0, v_x + u_y = 0.$
Você pode verificar que $\triangle = 4\frac{\partial}{\partial z} \frac{\partial}{\partial \bar{z}}$ e portanto as partes reais de imaginárias de qualquer função holomorfa é harmônica!
O conhecimento desse fato simples nos presenteia com um estoque gigantesco de funções harmônicas. Portanto dado $f(z)$ harmônica, $\log f(z)$ é harmônica também. Use a sua imaginação para criar outros exemplos.
Nós demonstramos que a parte real (ou imaginária) de toda função holomórfica é harmônica. Será que a recíproca é verdadeira? Em geral sim.
Teorema 1. Num domínio simplesmente conexo, toda função harmônica é a parte real de uma função analítica complexa, módulo uma constante puramente imaginária.
Nós queremos determinar $f = u + iv$, com $u$ dado.
Mas $u_x - v_y = 0$ e $u_y + v_x=0$,
e portanto
$v(x,y)$ = integral de linha de $\nabla v$ de $(x_0,y_0)$ fixo até $(x,y)$.
Mas $\nabla v = (-u_y,u_x)$ e as funções $u_x,u_y$ são dadas. Como o domínio é simplesmente conexo,
o valor da integral não depende do caminho e a única escolha feita foi o início do caminho de integração.
Portanto $v$ fica unicamente determinada módulo uma constante imaginária, como nós queriamos demonstrar.
Portanto a teoria das funções analíticas, e funções harmônicas (soluções da equação de Laplace) coincidem no plano.
Teorema 2. (O teorema do valor médio.) O valor médio de uma função harmônica ao longo de um círculo é igual ao valor dessa função no centro do círculo.
Suponha que o centro do círculo esteja localizado na origem, e suponha que o raio do círculo é $R$. Isso pode ser feito sem perda de generalidade.
Portanto, pela fórmula integral de Cauchy do cálculo complexo,
$f(0) = \frac{1}{2\pi i}\int_{\gamma} dz \frac{f(z)}{z} = \frac{1}{2\pi }\int_0^{2\pi} f(R\exp(i\phi)) d\phi$, e $f = u + i v$. Separando as partes reais e imaginárias nos dois lados da última igualdade nós obtemos o resultado desejado.
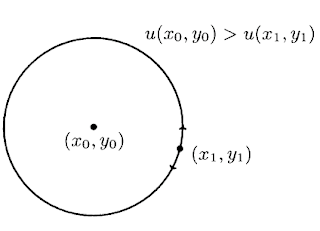
Corolário. Uma função harmônica não pode ter pontos de máximo ou mínimo (no sentido fraco) no interior do seu domínio de definição.
Vamos assumir que $u(x,y)$ não constante. Esse caso é trivial.
Ponto de máximo (resp. mínimo) fraco, e local significa que $u(x_0,y_0) \geq u(x,y)$ (resp. $\leq u(x,y)$) para todo $(x,y)$ próximo de $(x_0,y_0)$.
Considere um cículo pequeno ao redor de $(x_0,y_0)$. Então por continuidade a função é sempre menor em torno de um arco pequeno perto $(x_1,y_1)$ no círculo.
Portanto a média da função no círculo é menor que o valor da função no centro, uma contradição. Portanto a função é constante numa vizinhança de $(x_0,y_0)$. Portanto o conjunto dos pontos $\{(x,y): u(x_0,y_0) = u(x,y)\}$ é aberto e fechado.
Portanto como $D$ é conexo esse conjunto têm de coincidir com o domínio $D$ da função $u$, contradizendo nossa hipótese inicial. Portanto, se a função não é constante, e é harmônica a função não admite um máximo ou mínimo (fraco) global no interior do domínio. Quando a função têm uma extensão contínua para a fronteira, então como consequência o valores máximo e mínimos são realizados na fronteira.
Corolário. (Outro corolário do teorema do valor médio.) Seja $D$ um domínio limitado, com fronteira suave por partes. Seja $g$ uma função contínua na fronteira. Se existe $u$, harmônica em $D$ que se extende à $g$ na fronteira, então $u$ é única.
Em outras palavras, a solução do problema de Dirichlet, se ela existe ela á única.
Nenhum comentário:
Postar um comentário