quarta-feira, 9 de novembro de 2011
sexta-feira, 30 de setembro de 2011
Teoria potencial no plano e no espaço
Abaixo $x,x_i,y$ são todos vetores em $\mathbb{R}^3$.
O potencial gravitacional $\phi$ de uma partícula de massa $M$ num ponto situado a uma distância $x$ da partícula é
$\phi(x) = -G M/{\vert x\vert}$, onde $G$ é a constante gravitacional universal e $M$ é a massa da nossa partícula.
Daqui para frente nós vamos assumir que $G = 1$.
Dado um sistema de partículas posicionadas nos pontos $(x_i)_{i=0}^N$ o potencial gravitacional gerado por esse sistema de $N$ partículas é dado por
$\phi(x) = -\sum_{i=1}^N \frac{m_i}{\vert x - x_i\vert}.$
O mesmo vale para uma distribuição contínua de matéria,
e nesse caso o potential gravitacional vira $\phi(x) = \int_B \frac{dm(y)}{\vert y - x\vert} = \int_B dy \frac{\rho(y)}{\vert y - x\vert},$ onde $\rho(y)$ é função de densidade da distribuição de massa no corpo $B$.
Nessa última equação nós estamos supondo que $x,y$ são vetores bi-,tri-dimensionais etc. e que $dy$ é uma forma de volume, ou elemento de volume.
Vale a pena ressaltar aqui que o potential gravitacional em qualquer dos casos acima satisfaz a chamada equação de Poisson,
$$\triangle \phi = \rho(x),$$
onde $\triangle = \frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2} + \frac{\partial^2}{\partial z^2}$ é o operador de Laplace. Por quê? Consulte o seu livro favorito de mecânica clássica.
Portanto dada uma distribuição de massa $\rho(x)$ nós podemos tentar resolver para $\phi(x)$ para determinar o potencial gravitacional definido pelo corpo $B$. Pela mesma razão, o operador $\triangle$ aparece em eletromagnetismo clássico na determinação do potential elétrico definido por uma distribuição de cargas $\rho(x)$.
No caso de uma massa puntual, a densidade é uma função delta e $\rho(x) = \delta(x - x_0)$ onde $x_0$ é a localização da massa, ou carga no espaço.
A solução da equação de Laplace é para uma massa ou carga puntual é chamada de função de Green ou função de influência da carga em $x_0$.
No caso do operador de Laplace essa função de Green é exatamente o potencial gravitacional de uma partícula massiva ou carga puntual e é dada (módulo constantes de proporcionalidade) por $\phi(x) = \frac{1}{\vert x - x_0\vert}$.
Note que para uma distribuição de carga, ou de massa, contínua o potencial gravitacional é a convolução da função de Green com a distribuição de massa $\rho(x)$.
Vamos considerar agora as soluções da equação de Laplace no plano.
Isto é, em seguida nós vamos estudar a equação
$$u_{xx} + u_{yy} = 0,$$ ou ainda
$$(\frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2})u = 0.$$
Nós veremos em breve que existe uma relação profunda entre teoria potencial (soluções da equação de Laplace) e teoria de funções no plano complexo $\mathbb{C}$.
Para começar vamos recordar alguma notação do curso de cálculo complexo. Seja $z = x + \sqrt{-1}y$ onde $\sqrt{-1} = i$ é a constante imaginária.
No plano complexo $\mathbb{C}$ nós podemos definir dois operadores lineares,
$$\frac{\partial}{\partial z} = \frac{1}{2}(\frac{\partial}{\partial x} - i \frac{\partial}{\partial y} ),$$ e
$$\frac{\partial}{\partial \bar{z}} = \frac{1}{2}(\frac{\partial}{\partial x} + i \frac{\partial}{\partial y} ).$$
Nós dizemos que $f(z,\bar{z}) = u(x,y) + \sqrt{-1} v(x,y)$, diferenciável, é analítica (complexa) num aberto $U$ se
$\frac{\partial}{\partial \bar{z}} f(z,\bar{z})=0$ em $U$. Isso significa que $f = f(z)$ somente e que $f(z)$ (corolário) pode ser expandida como uma série de Taylor infinita em $z$ no aberto $U$. O aberto $U$ pode ser uma vizinhança (bola) de algum ponto $z_0$ fixo.
Funções analíticas complexas são também chamadas de holomorfas.
As partes real e imaginária da equação $\frac{\partial}{\partial \bar{z}} f(z,\bar{z})=0$ são exatamente as equações de Cauchy-Riemann do cálculo complexo:
$\frac{1}{2}(\frac{\partial}{\partial x} + i \frac{\partial}{\partial y} ) (u(x,y) + i v(x,y)) = 0 $
$\Rightarrow u_x - v_y = 0, v_x + u_y = 0.$
Você pode verificar que $\triangle = 4\frac{\partial}{\partial z} \frac{\partial}{\partial \bar{z}}$ e portanto as partes reais de imaginárias de qualquer função holomorfa é harmônica!
O conhecimento desse fato simples nos presenteia com um estoque gigantesco de funções harmônicas. Portanto dado $f(z)$ harmônica, $\log f(z)$ é harmônica também. Use a sua imaginação para criar outros exemplos.
Nós demonstramos que a parte real (ou imaginária) de toda função holomórfica é harmônica. Será que a recíproca é verdadeira? Em geral sim.
Teorema 1. Num domínio simplesmente conexo, toda função harmônica é a parte real de uma função analítica complexa, módulo uma constante puramente imaginária.
Nós queremos determinar $f = u + iv$, com $u$ dado.
Mas $u_x - v_y = 0$ e $u_y + v_x=0$,
e portanto
$v(x,y)$ = integral de linha de $\nabla v$ de $(x_0,y_0)$ fixo até $(x,y)$.
Mas $\nabla v = (-u_y,u_x)$ e as funções $u_x,u_y$ são dadas. Como o domínio é simplesmente conexo,
o valor da integral não depende do caminho e a única escolha feita foi o início do caminho de integração.
Portanto $v$ fica unicamente determinada módulo uma constante imaginária, como nós queriamos demonstrar.
Portanto a teoria das funções analíticas, e funções harmônicas (soluções da equação de Laplace) coincidem no plano.
Teorema 2. (O teorema do valor médio.) O valor médio de uma função harmônica ao longo de um círculo é igual ao valor dessa função no centro do círculo.
Suponha que o centro do círculo esteja localizado na origem, e suponha que o raio do círculo é $R$. Isso pode ser feito sem perda de generalidade.
A demonstração é a seguinte. Como nós sabemos, $u$ = parte real de $f(z)$ para algum $f(z)$ definido numa vizinhança gorda do disco limitado pelo círculo. .
Portanto, pela fórmula integral de Cauchy do cálculo complexo,
$f(0) = \frac{1}{2\pi i}\int_{\gamma} dz \frac{f(z)}{z} = \frac{1}{2\pi }\int_0^{2\pi} f(R\exp(i\phi)) d\phi$, e $f = u + i v$. Separando as partes reais e imaginárias nos dois lados da última igualdade nós obtemos o resultado desejado.
Corolário. Uma função harmônica não pode ter pontos de máximo ou mínimo (no sentido fraco) no interior do seu domínio de definição.
Vamos assumir que $u(x,y)$ não constante. Esse caso é trivial.
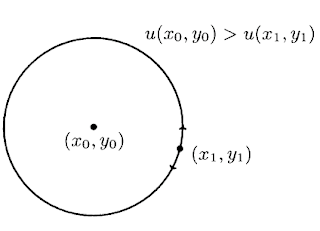
Ponto de máximo (resp. mínimo) fraco, e local significa que $u(x_0,y_0) \geq u(x,y)$ (resp. $\leq u(x,y)$) para todo $(x,y)$ próximo de $(x_0,y_0)$.
Considere um cículo pequeno ao redor de $(x_0,y_0)$. Então por continuidade a função é sempre menor em torno de um arco pequeno perto $(x_1,y_1)$ no círculo.
Portanto a média da função no círculo é menor que o valor da função no centro, uma contradição. Portanto a função é constante numa vizinhança de $(x_0,y_0)$. Portanto o conjunto dos pontos $\{(x,y): u(x_0,y_0) = u(x,y)\}$ é aberto e fechado.
Portanto como $D$ é conexo esse conjunto têm de coincidir com o domínio $D$ da função $u$, contradizendo nossa hipótese inicial. Portanto, se a função não é constante, e é harmônica a função não admite um máximo ou mínimo (fraco) global no interior do domínio. Quando a função têm uma extensão contínua para a fronteira, então como consequência o valores máximo e mínimos são realizados na fronteira.
Corolário. (Outro corolário do teorema do valor médio.) Seja $D$ um domínio limitado, com fronteira suave por partes. Seja $g$ uma função contínua na fronteira. Se existe $u$, harmônica em $D$ que se extende à $g$ na fronteira, então $u$ é única.
Em outras palavras, a solução do problema de Dirichlet, se ela existe ela á única.
O potencial gravitacional $\phi$ de uma partícula de massa $M$ num ponto situado a uma distância $x$ da partícula é
$\phi(x) = -G M/{\vert x\vert}$, onde $G$ é a constante gravitacional universal e $M$ é a massa da nossa partícula.
Daqui para frente nós vamos assumir que $G = 1$.
Dado um sistema de partículas posicionadas nos pontos $(x_i)_{i=0}^N$ o potencial gravitacional gerado por esse sistema de $N$ partículas é dado por
$\phi(x) = -\sum_{i=1}^N \frac{m_i}{\vert x - x_i\vert}.$
O mesmo vale para uma distribuição contínua de matéria,
e nesse caso o potential gravitacional vira $\phi(x) = \int_B \frac{dm(y)}{\vert y - x\vert} = \int_B dy \frac{\rho(y)}{\vert y - x\vert},$ onde $\rho(y)$ é função de densidade da distribuição de massa no corpo $B$.
Nessa última equação nós estamos supondo que $x,y$ são vetores bi-,tri-dimensionais etc. e que $dy$ é uma forma de volume, ou elemento de volume.
Vale a pena ressaltar aqui que o potential gravitacional em qualquer dos casos acima satisfaz a chamada equação de Poisson,
$$\triangle \phi = \rho(x),$$
onde $\triangle = \frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2} + \frac{\partial^2}{\partial z^2}$ é o operador de Laplace. Por quê? Consulte o seu livro favorito de mecânica clássica.
Portanto dada uma distribuição de massa $\rho(x)$ nós podemos tentar resolver para $\phi(x)$ para determinar o potencial gravitacional definido pelo corpo $B$. Pela mesma razão, o operador $\triangle$ aparece em eletromagnetismo clássico na determinação do potential elétrico definido por uma distribuição de cargas $\rho(x)$.
No caso de uma massa puntual, a densidade é uma função delta e $\rho(x) = \delta(x - x_0)$ onde $x_0$ é a localização da massa, ou carga no espaço.
A solução da equação de Laplace é para uma massa ou carga puntual é chamada de função de Green ou função de influência da carga em $x_0$.
No caso do operador de Laplace essa função de Green é exatamente o potencial gravitacional de uma partícula massiva ou carga puntual e é dada (módulo constantes de proporcionalidade) por $\phi(x) = \frac{1}{\vert x - x_0\vert}$.
Note que para uma distribuição de carga, ou de massa, contínua o potencial gravitacional é a convolução da função de Green com a distribuição de massa $\rho(x)$.
Vamos considerar agora as soluções da equação de Laplace no plano.
Isto é, em seguida nós vamos estudar a equação
$$u_{xx} + u_{yy} = 0,$$ ou ainda
$$(\frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2})u = 0.$$
Nós veremos em breve que existe uma relação profunda entre teoria potencial (soluções da equação de Laplace) e teoria de funções no plano complexo $\mathbb{C}$.
Para começar vamos recordar alguma notação do curso de cálculo complexo. Seja $z = x + \sqrt{-1}y$ onde $\sqrt{-1} = i$ é a constante imaginária.
No plano complexo $\mathbb{C}$ nós podemos definir dois operadores lineares,
$$\frac{\partial}{\partial z} = \frac{1}{2}(\frac{\partial}{\partial x} - i \frac{\partial}{\partial y} ),$$ e
$$\frac{\partial}{\partial \bar{z}} = \frac{1}{2}(\frac{\partial}{\partial x} + i \frac{\partial}{\partial y} ).$$
Nós dizemos que $f(z,\bar{z}) = u(x,y) + \sqrt{-1} v(x,y)$, diferenciável, é analítica (complexa) num aberto $U$ se
$\frac{\partial}{\partial \bar{z}} f(z,\bar{z})=0$ em $U$. Isso significa que $f = f(z)$ somente e que $f(z)$ (corolário) pode ser expandida como uma série de Taylor infinita em $z$ no aberto $U$. O aberto $U$ pode ser uma vizinhança (bola) de algum ponto $z_0$ fixo.
Funções analíticas complexas são também chamadas de holomorfas.
As partes real e imaginária da equação $\frac{\partial}{\partial \bar{z}} f(z,\bar{z})=0$ são exatamente as equações de Cauchy-Riemann do cálculo complexo:
$\frac{1}{2}(\frac{\partial}{\partial x} + i \frac{\partial}{\partial y} ) (u(x,y) + i v(x,y)) = 0 $
$\Rightarrow u_x - v_y = 0, v_x + u_y = 0.$
Você pode verificar que $\triangle = 4\frac{\partial}{\partial z} \frac{\partial}{\partial \bar{z}}$ e portanto as partes reais de imaginárias de qualquer função holomorfa é harmônica!
O conhecimento desse fato simples nos presenteia com um estoque gigantesco de funções harmônicas. Portanto dado $f(z)$ harmônica, $\log f(z)$ é harmônica também. Use a sua imaginação para criar outros exemplos.
Nós demonstramos que a parte real (ou imaginária) de toda função holomórfica é harmônica. Será que a recíproca é verdadeira? Em geral sim.
Teorema 1. Num domínio simplesmente conexo, toda função harmônica é a parte real de uma função analítica complexa, módulo uma constante puramente imaginária.
Nós queremos determinar $f = u + iv$, com $u$ dado.
Mas $u_x - v_y = 0$ e $u_y + v_x=0$,
e portanto
$v(x,y)$ = integral de linha de $\nabla v$ de $(x_0,y_0)$ fixo até $(x,y)$.
Mas $\nabla v = (-u_y,u_x)$ e as funções $u_x,u_y$ são dadas. Como o domínio é simplesmente conexo,
o valor da integral não depende do caminho e a única escolha feita foi o início do caminho de integração.
Portanto $v$ fica unicamente determinada módulo uma constante imaginária, como nós queriamos demonstrar.
Portanto a teoria das funções analíticas, e funções harmônicas (soluções da equação de Laplace) coincidem no plano.
Teorema 2. (O teorema do valor médio.) O valor médio de uma função harmônica ao longo de um círculo é igual ao valor dessa função no centro do círculo.
Suponha que o centro do círculo esteja localizado na origem, e suponha que o raio do círculo é $R$. Isso pode ser feito sem perda de generalidade.
A demonstração é a seguinte. Como nós sabemos, $u$ = parte real de $f(z)$ para algum $f(z)$ definido numa vizinhança gorda do disco limitado pelo círculo. .
Portanto, pela fórmula integral de Cauchy do cálculo complexo,
$f(0) = \frac{1}{2\pi i}\int_{\gamma} dz \frac{f(z)}{z} = \frac{1}{2\pi }\int_0^{2\pi} f(R\exp(i\phi)) d\phi$, e $f = u + i v$. Separando as partes reais e imaginárias nos dois lados da última igualdade nós obtemos o resultado desejado.
Corolário. Uma função harmônica não pode ter pontos de máximo ou mínimo (no sentido fraco) no interior do seu domínio de definição.
Vamos assumir que $u(x,y)$ não constante. Esse caso é trivial.
Ponto de máximo (resp. mínimo) fraco, e local significa que $u(x_0,y_0) \geq u(x,y)$ (resp. $\leq u(x,y)$) para todo $(x,y)$ próximo de $(x_0,y_0)$.
Considere um cículo pequeno ao redor de $(x_0,y_0)$. Então por continuidade a função é sempre menor em torno de um arco pequeno perto $(x_1,y_1)$ no círculo.
Portanto a média da função no círculo é menor que o valor da função no centro, uma contradição. Portanto a função é constante numa vizinhança de $(x_0,y_0)$. Portanto o conjunto dos pontos $\{(x,y): u(x_0,y_0) = u(x,y)\}$ é aberto e fechado.
Portanto como $D$ é conexo esse conjunto têm de coincidir com o domínio $D$ da função $u$, contradizendo nossa hipótese inicial. Portanto, se a função não é constante, e é harmônica a função não admite um máximo ou mínimo (fraco) global no interior do domínio. Quando a função têm uma extensão contínua para a fronteira, então como consequência o valores máximo e mínimos são realizados na fronteira.
Corolário. (Outro corolário do teorema do valor médio.) Seja $D$ um domínio limitado, com fronteira suave por partes. Seja $g$ uma função contínua na fronteira. Se existe $u$, harmônica em $D$ que se extende à $g$ na fronteira, então $u$ é única.
Em outras palavras, a solução do problema de Dirichlet, se ela existe ela á única.
sexta-feira, 23 de setembro de 2011
Lista de exercícios no. 3
1. Verifique a validade do princípio do máximo para a função harmônica
$u(x,y) = \frac{1-x^2-y^2}{1 - 2x + x^2 + y^2}$ no disco $\overline{D} = \{x^2 + y^2 \leq 1.\}$ Explique o seu raciocínio.
2. Qual a forma do Laplaciano em coordenadas polares? Verifique que
$$\Delta = \frac{\partial^2}{\partial r^2} + \frac{1}{r}\frac{\partial}{\partial r} + \frac{1}{r^2}\frac{\partial^2}{\partial r^2}.$$
Verifique também que $r^{\vert k\vert} \exp(ik\theta)$ é harmônica para todo $k$ inteiro.
3. Calcule todas as soluções da equação de Laplace que só dependem de $r$.
4. Suponha que $u$ é harmônica no interior do disco de raio $2$, i.e. em $D = \{ r < 2\}$ e que na fronteira assuma a forma $u = 3\sin(2\theta) + 1$. Sem calcular a função $u$ responda às seguintes questões:
(a) Qual o valor máximo de $u$ em $\overline{D}$?
(b) Qual o valor de $u$ na origem?
5. Resolva a equação de Laplace $\Delta u = 0$ no disco de raio $R$ com condição de fronteira $u = 1 + 3\sin(\theta)$.
6. (O método de Rayleigh-Ritz.)
Suponham que nós queremos resolver a equação de Laplace
num domínio limitado $D$, com condição de fronteira $u\vert_{\partial D} = h$ e sejam $(w_k)_{k=0}^N$ funções arbitrárias tais que $w_0\vert_{\partial D} = h$ e $u_{k\geq 1}\vert_{\partial D} = 0$.
Defina a forma de energia de Dirichlet,
$$E(u,v) = \int\int_{D}(\nabla u\bullet \nabla v) dx\wedge dy.$$
Nosso problema é encontrar constantes $(c_i)_{k=0}^N$ que $u_N = \sum_{k=0}^N c_k w_k$ minimiza $E(u_N,u_N)$.
O princípio de Dirichlet (que nós vamos discutir mais tarde no curso) diz que as soluções da equação de Laplace minimizam o funcional de energia acima.
Mostre que as constantes que resolvem o problema satisfazem $\sum_{k=1}^N E(w_j,w_k)c_k = - E(w_0,w_j), j = 1,2,\dots, N.$
7. Considere a equação de Laplace $\Delta u = u_{xx} + u_{yy} = 0$ no triângulo $$\{x>0,y>0, 3x + y < 3\}$$ e com condições de fronteira
$$u(x,0) = 0, u(0,y) = y(3-y), u(x,3-3x) = 0.$$
Escolha $w_0 = y(3-3x - y)$ e $w_1 = xy(3-3x-y)$. Encontre $u_1 = c_0 w_0 + c_1 w_1$ que melhor aproxima $u$ na norma da energia (de Dirichlet).
Isto é, encontre a aproximação de Rayleigh-Ritz de $u$ no triângulo acima.
Em seguida inclua um terceiro polinômio $w_2 = x^2 y (3 - 3x - y)$. Calcule uma aproximação da forma $u_2 = c_0 w_0 + c_1 w_1 + c_2 w_2$.
Será que a energia de $u_2$ é menor que a de $u_1$ acima?
8. (a) Se $u = f(x/y)$ é harmonica, resolva a equação diferencial que $f$ satisfaz.
(b) Mostre que $\frac{\partial}{\partial r}u = 0$.
(c) Mostre que $y>0$ e $\frac{\partial}{\partial r}v(r,\theta) = 0$ então $v$ é da forma $f(x/y)$.
(d) Encontre o limite $\lim_{y\to 0} u(x,y) = h(x)$.
9. (a) Use o exercício anterior para encontrar a função harmonica no semi-plano superior $\{y > 0\}$ que satisfaz $h(x) = 0$ se $x<0$ e $h(x) = 1$ se $x>0$.
(b) Seja $-\infty = a_0 < a_1 < a_2 < \dots < a_{N-1} < a_N = \infty$ uma partição da reta real, e seja $h(x) = \sum_{k=0}^N c_k \chi_k$ uma função escada.
A função $\chi_k$ é a função característica de $(a_k,a_{k+1})$.
Resolva a equação de Laplace em $\{y>0\}$ com condição de fronteira $h(x)$.
10. (Funcões de Green para problemas de fronteira.)
Considere $x_0 \in (0,l)$ onde $l$ é um parametro real positivo.
Encontre a unica função no intervalo $(0,l)$ que satisfaz
i. $G''(x) = 0$ se $x\neq 0 $;
ii. $G(0) = G(l) = 0$;
iii. $G(x)$ é continua em $x_0$ e $G(x) + \frac{1}{2}\vert x - x_0\vert$ é harmonica em $x_0$.
Lista 4 será sobre aplicações de teoria potential em eletrostática e gravitação.
$u(x,y) = \frac{1-x^2-y^2}{1 - 2x + x^2 + y^2}$ no disco $\overline{D} = \{x^2 + y^2 \leq 1.\}$ Explique o seu raciocínio.
2. Qual a forma do Laplaciano em coordenadas polares? Verifique que
$$\Delta = \frac{\partial^2}{\partial r^2} + \frac{1}{r}\frac{\partial}{\partial r} + \frac{1}{r^2}\frac{\partial^2}{\partial r^2}.$$
Verifique também que $r^{\vert k\vert} \exp(ik\theta)$ é harmônica para todo $k$ inteiro.
3. Calcule todas as soluções da equação de Laplace que só dependem de $r$.
4. Suponha que $u$ é harmônica no interior do disco de raio $2$, i.e. em $D = \{ r < 2\}$ e que na fronteira assuma a forma $u = 3\sin(2\theta) + 1$. Sem calcular a função $u$ responda às seguintes questões:
(a) Qual o valor máximo de $u$ em $\overline{D}$?
(b) Qual o valor de $u$ na origem?
5. Resolva a equação de Laplace $\Delta u = 0$ no disco de raio $R$ com condição de fronteira $u = 1 + 3\sin(\theta)$.
6. (O método de Rayleigh-Ritz.)
Suponham que nós queremos resolver a equação de Laplace
num domínio limitado $D$, com condição de fronteira $u\vert_{\partial D} = h$ e sejam $(w_k)_{k=0}^N$ funções arbitrárias tais que $w_0\vert_{\partial D} = h$ e $u_{k\geq 1}\vert_{\partial D} = 0$.
Defina a forma de energia de Dirichlet,
$$E(u,v) = \int\int_{D}(\nabla u\bullet \nabla v) dx\wedge dy.$$
Nosso problema é encontrar constantes $(c_i)_{k=0}^N$ que $u_N = \sum_{k=0}^N c_k w_k$ minimiza $E(u_N,u_N)$.
O princípio de Dirichlet (que nós vamos discutir mais tarde no curso) diz que as soluções da equação de Laplace minimizam o funcional de energia acima.
Mostre que as constantes que resolvem o problema satisfazem $\sum_{k=1}^N E(w_j,w_k)c_k = - E(w_0,w_j), j = 1,2,\dots, N.$
7. Considere a equação de Laplace $\Delta u = u_{xx} + u_{yy} = 0$ no triângulo $$\{x>0,y>0, 3x + y < 3\}$$ e com condições de fronteira
$$u(x,0) = 0, u(0,y) = y(3-y), u(x,3-3x) = 0.$$
Escolha $w_0 = y(3-3x - y)$ e $w_1 = xy(3-3x-y)$. Encontre $u_1 = c_0 w_0 + c_1 w_1$ que melhor aproxima $u$ na norma da energia (de Dirichlet).
Isto é, encontre a aproximação de Rayleigh-Ritz de $u$ no triângulo acima.
Em seguida inclua um terceiro polinômio $w_2 = x^2 y (3 - 3x - y)$. Calcule uma aproximação da forma $u_2 = c_0 w_0 + c_1 w_1 + c_2 w_2$.
Será que a energia de $u_2$ é menor que a de $u_1$ acima?
8. (a) Se $u = f(x/y)$ é harmonica, resolva a equação diferencial que $f$ satisfaz.
(b) Mostre que $\frac{\partial}{\partial r}u = 0$.
(c) Mostre que $y>0$ e $\frac{\partial}{\partial r}v(r,\theta) = 0$ então $v$ é da forma $f(x/y)$.
(d) Encontre o limite $\lim_{y\to 0} u(x,y) = h(x)$.
9. (a) Use o exercício anterior para encontrar a função harmonica no semi-plano superior $\{y > 0\}$ que satisfaz $h(x) = 0$ se $x<0$ e $h(x) = 1$ se $x>0$.
(b) Seja $-\infty = a_0 < a_1 < a_2 < \dots < a_{N-1} < a_N = \infty$ uma partição da reta real, e seja $h(x) = \sum_{k=0}^N c_k \chi_k$ uma função escada.
A função $\chi_k$ é a função característica de $(a_k,a_{k+1})$.
Resolva a equação de Laplace em $\{y>0\}$ com condição de fronteira $h(x)$.
10. (Funcões de Green para problemas de fronteira.)
Considere $x_0 \in (0,l)$ onde $l$ é um parametro real positivo.
Encontre a unica função no intervalo $(0,l)$ que satisfaz
i. $G''(x) = 0$ se $x\neq 0 $;
ii. $G(0) = G(l) = 0$;
iii. $G(x)$ é continua em $x_0$ e $G(x) + \frac{1}{2}\vert x - x_0\vert$ é harmonica em $x_0$.
Lista 4 será sobre aplicações de teoria potential em eletrostática e gravitação.
domingo, 18 de setembro de 2011
Gráfico de uma função harmônica
Esse é o gráfico da parte imaginária do função logaritmo $\log(z)$. Nessa figura nós estamos considerando o ramo da função logaritmo definida no plano menos o eixo real não positivo. O círculos na figura são as fronteiras de vizinhanças abertas, e o diagrama está ilustrando o processo de continuação analítica.
Outro exemplos interessantes são os gráficos da parte real e imaginárias de $\exp(z)$.
Outro exemplos interessantes são os gráficos da parte real e imaginárias de $\exp(z)$.
A fileira de baixo corresponde às curvas de nível da função. Tente verificar visualmente porque a propriedade do valor médio das funções harmônicas é verdadeira no caso da função exponencial.
sexta-feira, 16 de setembro de 2011
Sobre a escala de notas na prova P1
Nota máxima: 40 pontos.
26 pontos ou mais é excelente (> 90%);
16 pontos é bom (> 70%);
12 pontos é média ( > 50%).
26 pontos ou mais é excelente (> 90%);
16 pontos é bom (> 70%);
12 pontos é média ( > 50%).
Seminário QTP no. 2. Compareçam!
Essa segunda edição Q.T.P. será ministrada pelo Fred, conhecido de
todos pela sua dedicação e carinho à PUC:
Prof. Carlos Frederico Palmeira (departamento de Matemática, PUC-Rio):
http://www.mat.puc-rio.br/~
3a feira, dia 20/09, Sala 856L (sala de seminário do DMAT)
Topologia Simples Aplicada a Dinâmica dos Fluidos
- O estudo de um sistema de 2 equações diferenciais parciais que
aparece em mecânica de fluidos, leva a famílias de curvas a dois
parâmetros no plano, e isso por sua por sua vez leva a famílias, bem
mais simples, de curvas em uma superfície M de dimensão 3 mergulhada
em R4. Consideramos o caso em que as equações originais são bastante
simples (envolvendo polinômios de grau 2) e obtemos bastante
informação sobre a família de curvas em M, que podem ser transferidas
para as soluções do sistema original.
todos pela sua dedicação e carinho à PUC:
Prof. Carlos Frederico Palmeira (departamento de Matemática, PUC-Rio):
http://www.mat.puc-rio.br/~
3a feira, dia 20/09, Sala 856L (sala de seminário do DMAT)
Topologia Simples Aplicada a Dinâmica dos Fluidos
- O estudo de um sistema de 2 equações diferenciais parciais que
aparece em mecânica de fluidos, leva a famílias de curvas a dois
parâmetros no plano, e isso por sua por sua vez leva a famílias, bem
mais simples, de curvas em uma superfície M de dimensão 3 mergulhada
em R4. Consideramos o caso em que as equações originais são bastante
simples (envolvendo polinômios de grau 2) e obtemos bastante
informação sobre a família de curvas em M, que podem ser transferidas
para as soluções do sistema original.
quarta-feira, 14 de setembro de 2011
sexta-feira, 9 de setembro de 2011
A desigualdade de Bessel
Seja $f$ uma função contínua (ou mesmo contínua por partes) e seja $S_N(x) = \sum_{k=-N}^N c_k \exp(ikx)$ o polinômio de Fourier de grau de $N$.
É fácil mostrar que,
$(f - S_N,f - S_N) = \int_{-\pi}^{\pi}(f(x) - \sum_{k=-N}^N c_k \exp(ikx))(\bar{f}(x) - \sum_{k=-N}^N \bar{c}_k \exp(-ikx))dx =$
$\int_{-\pi}^{\pi}f(x)\bar{f}(x)dx - \sum_{k=-N}^N \vert c_k\vert^2 \geq 0.$
Portanto,
$ \int_{-\pi}^{\pi}f(x)\bar{f}(x)dx \geq \sum_{k=-N}^N \vert c_k\vert^2$ e tomando o limite quando $N\to \infty$ nós temos a desigualdade de Bessel.
Isso implica em particular que $c_k \to 0$ quando $k\to \infty$ ou $\lim_{k\to \infty}f(x) \exp(ikx) dx = 0$, que é uma forma particular do lema de Riemann-Lebesgue.
Isso é bastante útil em demonstrações envolvendo integrais oscilatórias.
É fácil mostrar que,
$(f - S_N,f - S_N) = \int_{-\pi}^{\pi}(f(x) - \sum_{k=-N}^N c_k \exp(ikx))(\bar{f}(x) - \sum_{k=-N}^N \bar{c}_k \exp(-ikx))dx =$
$\int_{-\pi}^{\pi}f(x)\bar{f}(x)dx - \sum_{k=-N}^N \vert c_k\vert^2 \geq 0.$
Portanto,
$ \int_{-\pi}^{\pi}f(x)\bar{f}(x)dx \geq \sum_{k=-N}^N \vert c_k\vert^2$ e tomando o limite quando $N\to \infty$ nós temos a desigualdade de Bessel.
Isso implica em particular que $c_k \to 0$ quando $k\to \infty$ ou $\lim_{k\to \infty}f(x) \exp(ikx) dx = 0$, que é uma forma particular do lema de Riemann-Lebesgue.
Isso é bastante útil em demonstrações envolvendo integrais oscilatórias.
terça-feira, 6 de setembro de 2011
Testinho 2
O testinho tinha duas partes, a primeira parte consistia em calcular
Veja o livro do Lighthill, "Introduction to Fourier Analysis and Generalized Functions."
O problema maior aqui é definir o espaço de funções onde o funcional linear $\delta(x)$ atua.
Lighthill assume que $\delta(x)$ mora no espaço de boas funções,
funções $C^{\infty}$ que caem bastante rápido quando $x\to \infty$. De fato, mais rápido que qualquer polinômio.
$F(x) = \frac{\exp(-\frac{x^2}{2\sigma}) }{\sqrt{2\pi\sigma}}*\frac{\exp(-\frac{x^2}{2\tau}) }{\sqrt{2\pi\tau}},$
onde $\tau,\sigma$ são ambas constantes positivas.
A segunda parte pedia para verificar que $\int_{\mathbb{R}}\frac{\exp(-\frac{x^2}{2\sigma}) }{\sqrt{2\pi\sigma}} dx = 1$ e que $\lim_{\sigma\to 0} \frac{\exp(-\frac{x^2}{2\sigma}) }{\sqrt{2\pi\sigma}} = \delta(x)$ no sentido fraco.
O truque na primeira parte era se lembrar que se $f(x) = \frac{\exp(-\frac{x^2}{2\sigma}) }{\sqrt{2\pi\sigma}}$, então $\frac{d f}{dx}(x) = - \frac{x}{\sigma}f(x)$ e portanto $\sigma ik \widehat{f}(k) = -i \frac{d\widehat{f}}{dk}(k) \Rightarrow \widehat{f}(k) \propto \exp(-\sigma k^2/2)$ pelas propriedades da transformada de Fourier, e a constante de proporcionalidade à direita não depende de $\sigma$. (Por quê? Veja a segunda parte. )
De qualquer forma, pelo teorema de convolução
$\widehat{f(x)*g(x)} = 2\pi \widehat{f}(k) \widehat{g}(k)$ e portanto
$\widehat{F}(k) = \frac{1}{2\pi} \exp(-\sigma k^2/2) \exp(-\tau k^2/2) = \exp(-(\sigma + \tau) k^2/2)$ e tomando a transformada inversa, $F(x) = \frac{\exp(-\frac{x^2}{2(\sigma + \tau)}) }{\sqrt{2\pi(\sigma + \tau)}}.$
Para verificar que $\int_{\mathbb{R}} \frac{\exp(-\frac{x^2}{2\sigma}) }{\sqrt{2\pi\sigma}} dx = 1$ basta escalonar a variável de integração e se lembrar que $\int_{\mathbb{R}}\exp(-x^2/2)dx = \sqrt{2\pi}$.
A última parte do problema pedia para mostrar que $\lim_{\sigma\to 0} \frac{\exp(-\frac{x^2}{2\sigma}) }{\sqrt{2\pi\sigma}} = \delta(x)$ no sentido fraco.
A última parte foi de fato um desafio.
A maneira indireta,
se $f(x) = \frac{\exp(-\frac{x^2}{2\sigma}) }{\sqrt{2\pi\sigma}}$ e $g(x) = \overline{f}*f $ (ou $f*f$ se $f$ for real) então
$\widehat{g}(k)=\widehat{\overline{f}*f} = \overline{\widehat{f}(k)} \widehat{f}(k) = \vert \widehat{f}(k)\vert^2$.
Pela fórmula de inversão,
$g(x) = \int_{\mathbb{R}}\vert \widehat{f}(k)\vert^2 \exp(ikx) dk \Rightarrow g(0) = \int \vert f(x) \vert^2 dx = \int_{\mathbb{R}}\vert \widehat{f}(k)\vert^2 dk$.
Essas manipulações formais dependem de $f$ e $\widehat{f}$ serem ambas quadrado integráveis.
Fica fácil provar agora que $\int f(x) g(x) dx = \int \widehat{f}(k) \widehat{g}(k) dk.$
Portanto no sentido fraco nós temos que
$\int \frac{\exp(-\frac{x^2}{2\sigma}) }{\sqrt{2\pi\sigma}} \phi(x) dx = \int \frac{1}{2\pi} \exp(-\sigma k^2/2) \widehat{\phi}(k) dk$,
e quando $\sigma \to 0$ o lado direito tende à $\propto \int_{\mathbb{R}} \widehat{\phi}(k) dk = \phi(0)$ pela fórmula de inversão.
Conclusão: o limite fraco de $\exp(-\frac{x^2}{2\sigma})$ é a função $\delta$ vezes uma constante.
A maneira direta pode ser argumentada assim.
Como nós mencionamos no enunciado do problema, a medida que $\sigma \to 0$ o gráfico de $\frac{\exp(-\frac{x^2}{2\sigma}) }{\sqrt{2\pi\sigma}}$ fica mais alto e mais fino.
Nós vamos primeiro demonstrar que a a cauda do gráfico contribui pouco para a área total.
Para $x \geq 2\epsilon$, $x^2/2\epsilon \geq x/2\epsilon$ e como $\exp(-t)$ é decrescente,
$\exp(-x^2/2\epsilon) \leq \exp(-x/2\epsilon)$.
Portanto,
$\int_{2\epsilon}^{\infty}\frac{\exp(-\frac{x^2}{2\epsilon}) }{\sqrt{2\pi\epsilon}} dx \leq \int_{2\epsilon}^{\infty}\frac{\exp(-\frac{x}{2\epsilon}) }{\sqrt{2\pi\epsilon}} dx = c \epsilon^{1/2}.$
Nós podemos concluir que a área $\int_{\vert x\vert \geq 2\epsilon} \exp(-x^2/2\epsilon) dx \leq c \epsilon^{1/2}.$
Agora como exercício tente se convencer que
$\lim_{\epsilon \to 0} f_{\epsilon}(x) \phi(x) dx = \phi(0)$, onde
$f_{\epsilon}(x) = \frac{\exp(-\frac{x^2}{2\epsilon}) }{\sqrt{2\pi\epsilon}}$.
Veja o livro do Lighthill, "Introduction to Fourier Analysis and Generalized Functions."
O problema maior aqui é definir o espaço de funções onde o funcional linear $\delta(x)$ atua.
Lighthill assume que $\delta(x)$ mora no espaço de boas funções,
funções $C^{\infty}$ que caem bastante rápido quando $x\to \infty$. De fato, mais rápido que qualquer polinômio.
sexta-feira, 2 de setembro de 2011
A transformada de Fourier: parte 2 (algumas considerações técnicas)
Nessa aula (24/08/2011) nosso objetivo foi demonstrar a fórmula de invesão de Fourier,
$f(x) = \frac{1}{2\pi}\int_{-\infty }^{\infty}dk \left( \int_{-\infty}^{\infty} dt f(x) \exp(-ik(t-x))\right).$
Antes de nos aventurarmos na demonstração e tecnicalidades da prova, vamos motivar primeiro a noção de integral Fourier como um limite formal de uma série de Fourier de uma função de período $L$, com $L\to \infty$.
Considere primeiro a função $f_L(x)$ que coincide com a função original $f(x)$ no intervalo $[-L/2,L/2]$ e é zero fora dela.
A série de Fourier da extensão $L$-periódica dessa função é $f_L(x) =\sum_{k=-\infty}^{\infty}c_k\exp(\frac{2\pi i k x}{L}),$ onde cada $c_k = \frac{1}{L}\int_{-L/2}^{L/2}f(t)\exp(\frac{-2\pi i k t}{L}) dt.$
Portanto,
$f_L(x) = \sum_{k=-\infty}^{\infty}( \frac{1}{L}\int_{-L/2}^{L/2}f(t)\exp(\frac{-2\pi i k t}{L}) dt)\exp(\frac{2\pi i k x}{L}),$
$= \frac{1}{L}\sum_{k=-\infty}^{\infty}\int_{-\infty}^{\infty}f(t)\exp(\frac{2\pi i k (t - x)}{L})dt.$
Considere agora a função $F(\lambda) = \int_{-L/2}^{L/2 } f(t) \exp(-i\lambda (t-x))dt$ (assumindo que $x$ é uma constante, ou que $x$ foi fixado antes. Essa função auxiliar nos permite ver a expressão
$\frac{1}{L}\sum_{k=-\infty}^{\infty}\int_{-\infty}^{\infty}f(t)\exp(\frac{2\pi i k (t - x)}{L})dt = \frac{1}{2\pi}\sum_{-\infty}^{\infty}F(\lambda_k) \Delta \lambda,$
onde $\lambda_k = \frac{2\pi k}{L}$ e $\Delta \lambda = \frac{2\pi}{L}$. Isto é, a somatória infinita é uma soma de Riemann da função $F(\lambda)$. A razão para escolhermos $\Delta \lambda = \frac{2\pi}{L}$ é porque quando $k$ varia por uma unidade a freqüência $ \lambda$ varia por $\Delta \lambda = 2\pi/L$.
O limite formal $L\to \infty$ nos dá a fórmula de inversão de Fourier.
O teorema que nós vamos provar é o seguinte,
Teorema. Seja $f(x) \in L^1(\mathbb{R})$ e suponha que $f(x)$ seja $C^2(\mathbb{R})$. Então
$f(x) = \int_{-\infty }^{\infty}dk \left( \int_{-\infty}^{\infty} dt f(t) \exp(-ik(t-x))\right).$
Algumas observações antes de procedermos com a demonstração do teorema. A condição $f(x)\in C^2(\mathbb{R})$ é bem restritiva. Na verdade a maioria dos livros de análise é suficiente assumirmos que $f(x)$ é Dini contínuo ou Lipshitz contínuo. Se a função for Lipshitz contínua, ela é Dini contínua. A noção de continuidade no sentido de Dini é um refinamento da noção de continuidade.
Lendo a Mathematical Encyclopedia da Springer, Dini continuidade significa que
$\lim_{\delta\to 0+}\omega(f;\delta) \log(1/\delta) = 0,$
$\omega(f;\delta) = \sup_{\vert x-y\vert \leq \delta} \vert f(x) - f(y)\vert$. Essa última quantidade é chamada o modulo de variação da função para uma variação em $\delta$ no argumento.
O crescimento de $\log(1/\delta)$ é muito lento, e portanto a condição de Dini é uma restrição na variação de $f$. (A variação de $f$ é "sublogrítmica.") Para nós, Lipshitz é suficiente, já que Lipshitz implica Dini.
Mais tarde, durante a demonstração nós veremos onde a condição de Dini é necessária.
Prova do teorema.
Definina $F_L(x) = \frac{1}{2\pi} \int_{-L}^{L}dk \left( \int_{-\infty}^{\infty} dt f(x) \exp(-ik(t-x))\right).$
Nós vamos mostrar que $F_L(x)$ tende à $f(x)$ uniformemente.
Aplicando o teorema de Fubini em
$F_L(x) = \frac{1}{2\pi} \left( \int_{-\infty}^{\infty} dt \int_{-L}^{L}dk f(t) \exp(-ik(t-x))\right).$
Isso é possível porquê $f(t) \exp(-ik(t-x))$ é absolutamente integrável na fita $[-A,A]\times [-\infty,\infty]$. (Por quê?)
Na nova ordem de integração,
$F_L(x) = \frac{1}{2\pi} \left( \int_{-\infty}^{\infty} dt f(t) \int_{-L}^{L}dk \exp(-ik(t-x))\right)$
$=\frac{1}{2\pi} \left( \int_{-\infty}^{\infty} dt f(t) \int_{-L}^{L}dk \exp(-ik(t-x))\right)$
$=\frac{1}{2\pi} \left( \int_{-\infty}^{\infty} dt f(t) \frac{2\sin(L(t-x))}{(t-x)}\right)$
$=\frac{1}{\pi} \left( \int_{-\infty}^{\infty} dz f(x+z) \frac{\sin(Lz)}{z}\right),$
onde a última igualdade foi obtida através de uma mudança de coordenadas linear $z = t-x$.
Agora, nós sabemos que, através de integrais de linha é possível provar que
$\int_{-\infty}^{\infty}dz \sin(z)/z = \pi$.
Dado $\epsilon > 0$ arbitrário nós vamos escolher $R \gg 1$ e $L \gg 1$ tal que o valor absoluto de cada um dos termos no lado direito em
$F_L(x) - f(x) = \frac{1}{\pi}\int_{\vert z\vert \leq R}dz \frac{f(x+z) - f(x)}{z}\sin(Lz) + \frac{1}{\pi}\int_{\vert z\vert > R} dz f(x+z) \frac{\sin(Lz)}{z} - f(x) \frac{1}{\pi}\int_{\vert z\vert > R} dz \frac{\sin(Lz)}{z}$
é menos que $\epsilon/3$. Estimando cada um dos termos no lado direito,
Portanto a diferença $F_L(x) - f(x)$ tende à zero.
A transformada de Fourier têm várias propriedades importantes, entre elas,
$f(x) = \frac{1}{2\pi}\int_{-\infty }^{\infty}dk \left( \int_{-\infty}^{\infty} dt f(x) \exp(-ik(t-x))\right).$
Antes de nos aventurarmos na demonstração e tecnicalidades da prova, vamos motivar primeiro a noção de integral Fourier como um limite formal de uma série de Fourier de uma função de período $L$, com $L\to \infty$.
Considere primeiro a função $f_L(x)$ que coincide com a função original $f(x)$ no intervalo $[-L/2,L/2]$ e é zero fora dela.
A série de Fourier da extensão $L$-periódica dessa função é $f_L(x) =\sum_{k=-\infty}^{\infty}c_k\exp(\frac{2\pi i k x}{L}),$ onde cada $c_k = \frac{1}{L}\int_{-L/2}^{L/2}f(t)\exp(\frac{-2\pi i k t}{L}) dt.$
Portanto,
$f_L(x) = \sum_{k=-\infty}^{\infty}( \frac{1}{L}\int_{-L/2}^{L/2}f(t)\exp(\frac{-2\pi i k t}{L}) dt)\exp(\frac{2\pi i k x}{L}),$
$= \frac{1}{L}\sum_{k=-\infty}^{\infty}\int_{-\infty}^{\infty}f(t)\exp(\frac{2\pi i k (t - x)}{L})dt.$
Considere agora a função $F(\lambda) = \int_{-L/2}^{L/2 } f(t) \exp(-i\lambda (t-x))dt$ (assumindo que $x$ é uma constante, ou que $x$ foi fixado antes. Essa função auxiliar nos permite ver a expressão
$\frac{1}{L}\sum_{k=-\infty}^{\infty}\int_{-\infty}^{\infty}f(t)\exp(\frac{2\pi i k (t - x)}{L})dt = \frac{1}{2\pi}\sum_{-\infty}^{\infty}F(\lambda_k) \Delta \lambda,$
onde $\lambda_k = \frac{2\pi k}{L}$ e $\Delta \lambda = \frac{2\pi}{L}$. Isto é, a somatória infinita é uma soma de Riemann da função $F(\lambda)$. A razão para escolhermos $\Delta \lambda = \frac{2\pi}{L}$ é porque quando $k$ varia por uma unidade a freqüência $ \lambda$ varia por $\Delta \lambda = 2\pi/L$.
O limite formal $L\to \infty$ nos dá a fórmula de inversão de Fourier.
O teorema que nós vamos provar é o seguinte,
Teorema. Seja $f(x) \in L^1(\mathbb{R})$ e suponha que $f(x)$ seja $C^2(\mathbb{R})$. Então
$f(x) = \int_{-\infty }^{\infty}dk \left( \int_{-\infty}^{\infty} dt f(t) \exp(-ik(t-x))\right).$
Algumas observações antes de procedermos com a demonstração do teorema. A condição $f(x)\in C^2(\mathbb{R})$ é bem restritiva. Na verdade a maioria dos livros de análise é suficiente assumirmos que $f(x)$ é Dini contínuo ou Lipshitz contínuo. Se a função for Lipshitz contínua, ela é Dini contínua. A noção de continuidade no sentido de Dini é um refinamento da noção de continuidade.
Lendo a Mathematical Encyclopedia da Springer, Dini continuidade significa que
$\lim_{\delta\to 0+}\omega(f;\delta) \log(1/\delta) = 0,$
$\omega(f;\delta) = \sup_{\vert x-y\vert \leq \delta} \vert f(x) - f(y)\vert$. Essa última quantidade é chamada o modulo de variação da função para uma variação em $\delta$ no argumento.
O crescimento de $\log(1/\delta)$ é muito lento, e portanto a condição de Dini é uma restrição na variação de $f$. (A variação de $f$ é "sublogrítmica.") Para nós, Lipshitz é suficiente, já que Lipshitz implica Dini.
Mais tarde, durante a demonstração nós veremos onde a condição de Dini é necessária.
Prova do teorema.
Definina $F_L(x) = \frac{1}{2\pi} \int_{-L}^{L}dk \left( \int_{-\infty}^{\infty} dt f(x) \exp(-ik(t-x))\right).$
Nós vamos mostrar que $F_L(x)$ tende à $f(x)$ uniformemente.
Aplicando o teorema de Fubini em
$F_L(x) = \frac{1}{2\pi} \left( \int_{-\infty}^{\infty} dt \int_{-L}^{L}dk f(t) \exp(-ik(t-x))\right).$
Isso é possível porquê $f(t) \exp(-ik(t-x))$ é absolutamente integrável na fita $[-A,A]\times [-\infty,\infty]$. (Por quê?)
Na nova ordem de integração,
$F_L(x) = \frac{1}{2\pi} \left( \int_{-\infty}^{\infty} dt f(t) \int_{-L}^{L}dk \exp(-ik(t-x))\right)$
$=\frac{1}{2\pi} \left( \int_{-\infty}^{\infty} dt f(t) \int_{-L}^{L}dk \exp(-ik(t-x))\right)$
$=\frac{1}{2\pi} \left( \int_{-\infty}^{\infty} dt f(t) \frac{2\sin(L(t-x))}{(t-x)}\right)$
$=\frac{1}{\pi} \left( \int_{-\infty}^{\infty} dz f(x+z) \frac{\sin(Lz)}{z}\right),$
onde a última igualdade foi obtida através de uma mudança de coordenadas linear $z = t-x$.
Agora, nós sabemos que, através de integrais de linha é possível provar que
$\int_{-\infty}^{\infty}dz \sin(z)/z = \pi$.
Dado $\epsilon > 0$ arbitrário nós vamos escolher $R \gg 1$ e $L \gg 1$ tal que o valor absoluto de cada um dos termos no lado direito em
$F_L(x) - f(x) = \frac{1}{\pi}\int_{\vert z\vert \leq R}dz \frac{f(x+z) - f(x)}{z}\sin(Lz) + \frac{1}{\pi}\int_{\vert z\vert > R} dz f(x+z) \frac{\sin(Lz)}{z} - f(x) \frac{1}{\pi}\int_{\vert z\vert > R} dz \frac{\sin(Lz)}{z}$
é menos que $\epsilon/3$. Estimando cada um dos termos no lado direito,
- $\vert \frac{1}{\pi}\int_{\vert z\vert \leq R}dz \frac{f(x+z) - f(x)}{z}\sin(Lz)\vert < \epsilon/3$ se $L \gg 1$ pois $\frac{f(x+z) - f(x)}{z}$ é contínua e limitada, e pelo lema de Riemann-Lebesgue se a freqüência $L$ for muito grande, a integral oscilatória tende à zero;
- $f(x)$ sendo absolutamente integrável implica que $\vert \frac{f(x+z)\sin(Lz)}{z}\vert \leq \vert \frac{f(x+z)}{z} \vert \leq \vert f(x+z)\vert$ é integrável no domínio $\vert z\vert \geq R$ e é tão pequena quanto quisermos, por exemplo $\epsilon/3$ se $R$ for suficientemente grande;
- a última integral também pode ser feita pequena se $R$ for grande.
Portanto a diferença $F_L(x) - f(x)$ tende à zero.
A transformada de Fourier têm várias propriedades importantes, entre elas,
- se $(f_n)$ é uma sequência de Cauchy na norma $L_1(\mathbb{R})$ a sequência $\widehat{f}_n$ é Cauchy na norma de convergência uniforme.
- Se $f\in L_1(\mathbb{R})$ então $\widehat{f}$ é contínua e limitada. (Não necessáriamente absolutamente integrável.)
- Se $f$ é absolutamente contínua (a derivada existe em quase todo ponto, e o teorema fundamental do Cálculo aplica) e $f'$ é absolutamente integrável então $\widehat{f'} = ik \widehat{f}$. Em particular, argumentando por indução, nós podemos provar que $\vert \widehat{f}\vert \leq C/\vert k\vert^r$ onde $r$ é a ordem de diferenciabilidade de $f$. (Assumindo que as derivadas apropriadas são integráveis.)
- Se $f(x),xf(x)\in L_1(\mathbb{R})$ então $\frac{d}{dk}\widehat{f} = \widehat{-ixf(x)}$.
- Se $\exp(\delta \vert x\vert) f(x) \in L_1(\mathbb{R})$ então $\widehat{f}$ é analítica.
O único comentário que eu vou fazer é sobre a demonstração do item (2). Prove que o teorema é verdadeiro para funções características de intervalos abertos na reta real, e por linearidade, para qualquer função escada de suporte compacto. Em seguida você teria que demonstrar que as funções escadas de suporte limitado são densas no espaço de funções (abs.) integráveis na reta toda. A continuidade da transformada de Fourier (i.e. (1)) conclui a demonstração.
terça-feira, 30 de agosto de 2011
A transformada de Fourier no espaço $\mathcal{L}_1$
Consultando o livro da Valéria Iório, eu percebi que para fins pedagógicos é razoável introduzir a transformada de Fourier para funções integráveis em qualquer intervalo $[a,b]$ e que satisfazem
$\lim_{R\to \infty} \int_{[-R,R]}\vert f(x)\vert dx < \infty$. A Valéria chama esse espaço de $\mathcal{L}_1$.
Nesse espaço fica fácil ver que as funçoes escada, isto é, combinações lineares finitas de funções características é denso. Isso é consêquencia imediata da definição de integral de Riemann.
Outro comentário parentético, o Daniel Sampaio bem-observou ontem que na prova que $\widehat{f'}(k) = ik \widehat{f}(k)$ nós não precisamos assumir que ambas $f,f'$ são absolutamente integráveis, mas somente que $f'$ é, e que $f$ é absolutamente contínua.
$\lim_{R\to \infty} \int_{[-R,R]}\vert f(x)\vert dx < \infty$. A Valéria chama esse espaço de $\mathcal{L}_1$.
Nesse espaço fica fácil ver que as funçoes escada, isto é, combinações lineares finitas de funções características é denso. Isso é consêquencia imediata da definição de integral de Riemann.
Outro comentário parentético, o Daniel Sampaio bem-observou ontem que na prova que $\widehat{f'}(k) = ik \widehat{f}(k)$ nós não precisamos assumir que ambas $f,f'$ são absolutamente integráveis, mas somente que $f'$ é, e que $f$ é absolutamente contínua.
segunda-feira, 29 de agosto de 2011
Lista de exercícios 2: continuação
3. Repita a demonstração em aula do teorema de convolução para demonstrar que a transformada (inversa) de $\widehat{f}(k)\widehat{g}(k)$ é $f\star g$, onde $\star$ é o produto de convolução.
4. Esboçe o gráfico de $g = f\star f$, onde $f$ é o pulso quadrado,
$f(x) = \left\{\begin{array}{ll}
1, & \vert x\vert \leq 1/2 \\
0,& \vert x\vert > 1/2.
\end{array}.
\right. $
Calcule $h = f\star f\star f$. Esboçe o gráfico aqui também.
5. Seja $\delta_N$ a sequência do tipo delta $\delta_N(x) = \left\{ \begin{array}{ll} N, & \vert x\vert \leq \frac{1}{2N} \\
0, & \vert x\vert > \frac{1}{2N}
\end{array}.
\right.$
4. Esboçe o gráfico de $g = f\star f$, onde $f$ é o pulso quadrado,
$f(x) = \left\{\begin{array}{ll}
1, & \vert x\vert \leq 1/2 \\
0,& \vert x\vert > 1/2.
\end{array}.
\right. $
Calcule $h = f\star f\star f$. Esboçe o gráfico aqui também.
5. Seja $\delta_N$ a sequência do tipo delta $\delta_N(x) = \left\{ \begin{array}{ll} N, & \vert x\vert \leq \frac{1}{2N} \\
0, & \vert x\vert > \frac{1}{2N}
\end{array}.
\right.$
Mostre que $\lim_{N\to \infty} \widehat{\delta_N}(k) = 1.$ Isso mostra que a transformada de Fourier da função $\delta(x)$ (o delta de Dirac) é, como um limite fraco, identicamente 1.
6. Seja $f(x) = \exp(-a x^2), a > 0$.
O integrando da integral $\widehat{f}(k) = \frac{1}{2\pi}\int_{-\infty}^{\infty}\exp(-ax^2 - ikx) dx$ é analítico e não contém nenhuma singularidade na parte finita do plano.
O valor dessa integral para cada $k$ não muda se ao invés de integrarmos na reta real nós integrarmos ao longo da reta $z(t) = \sigma + i t, \sigma \in \mathbb{R}$. (Teorema de Cauchy para integração complexa.)
Portanto,
rescreva a integral de Fourier como uma integral ao longo da reta $z(t) = \sigma + it$. Sabendo que $\int_{\mathbb{R}} \exp(-a x^2) dx= \sqrt{\frac{\pi}{a}}$ calcule a transformada de $f(x)$.
7. (A equação do calor) Considere a equação do calor,
$$u_t(x,t) - u_{xx}(x,t) = 0,$$ $t\geq 0$ e $x\in (-\infty,\infty)$. O problema de Cauchy para essa equação pede que dados $u_0(t)$ nós calculemos $u(x,t)$ para $t\geq 0$. Aplique a transformada de Fourier (com respeito à $x$) e obtenha uma equação diferencial ordinária para $\widehat{u}(k)$. Assuma que $u(x,t)$ é boa o sufficiente de tal forma que as operações $\frac{\partial}{\partial t}(\dots)$ e $\int_{\infty}^{\infty}(\dots)$ comutem.
Utilize o exercício anterior para calcular a transformação inversa (com respeito à $k$) de $\widehat{u}(k,t)$.
Lembre-se que $u(x,0) = u_0(x)$ e portanto $\widehat{u}(k,0) = \widehat{u_0}(k)$.
Como fica a solução anterior se $u_0(x) = \delta(x)$ ou $\delta(x-a)$?
8. Prova elementar do teorema de convergência de Fourier. O autor é o professor P. Chernoff.
(a) Seja $f(x)$ uma função $C^1$ de período $2\pi$ e suponha que $f(0) = 0$. Nos próximos items nos vamos demonstrar que a série de Fourier da função converge em $x = 0$ para $f(0)=0$. Em seguida nós demonstraremos que ela converge para qualquer ponto no domínio fundamental $[0,2\pi]$.
(b) Seja $g(x) = f(x)/(\exp(ix) - 1)$. Mostre que $ lim_{x\to 0} g(x)$ existe e defina $g(0)$ como sendo esse limite. Isso amarra a função em $x = 0$, garantindo continuidade. Como ambos o numerador e o denominador são $2\pi$ periódicos, nós teremos então uma função contínua e periódica na reta toda.
A função sendo contínua no intervalo $[0,2\pi]$ os coefficientes de Fourier são bem-definidos.
(c) Seja $c_k$ e $d_k$ os coeficientes de Fourier de $f(x)$ e $g(x)$ respectivamente. Mostre que
$d_k \to 0$ quando $k\to \infty$.
Minha dica, use o lema de Riemann-Lebesgue.
(d) Mostre que $c_k = d_k - d_{k-1}$ e portanto a série $\sum c_k$ é telescópica.
(e) Conclua a demonstração, isto é, mostre que $\sum c_k = 0$.
Isto é, mostre que $\sum_{k=-N}^N c_k \to 0$ quando $N \to \infty.$
(f) Seja $h(x) = f(x + x_0) - f(x_0)$. Então $h$ é $C^1$, periódica e satisfaz $h(0) = 0$.
Conclua que se $\sum c_k \exp(ik x)$ é a série de Fourier de $f$ então, $\sum c_k \exp(ik x_0) = f(x_0$.
Obs.: esse exercício só demonstra convergência puntual.
Anteriormente nós tinhamos demonstrado convergência uniforme no caso em que $f$ era $C^2$.
8. Prova elementar do teorema de convergência de Fourier. O autor é o professor P. Chernoff.
(a) Seja $f(x)$ uma função $C^1$ de período $2\pi$ e suponha que $f(0) = 0$. Nos próximos items nos vamos demonstrar que a série de Fourier da função converge em $x = 0$ para $f(0)=0$. Em seguida nós demonstraremos que ela converge para qualquer ponto no domínio fundamental $[0,2\pi]$.
(b) Seja $g(x) = f(x)/(\exp(ix) - 1)$. Mostre que $ lim_{x\to 0} g(x)$ existe e defina $g(0)$ como sendo esse limite. Isso amarra a função em $x = 0$, garantindo continuidade. Como ambos o numerador e o denominador são $2\pi$ periódicos, nós teremos então uma função contínua e periódica na reta toda.
A função sendo contínua no intervalo $[0,2\pi]$ os coefficientes de Fourier são bem-definidos.
(c) Seja $c_k$ e $d_k$ os coeficientes de Fourier de $f(x)$ e $g(x)$ respectivamente. Mostre que
$d_k \to 0$ quando $k\to \infty$.
Minha dica, use o lema de Riemann-Lebesgue.
(d) Mostre que $c_k = d_k - d_{k-1}$ e portanto a série $\sum c_k$ é telescópica.
(e) Conclua a demonstração, isto é, mostre que $\sum c_k = 0$.
Isto é, mostre que $\sum_{k=-N}^N c_k \to 0$ quando $N \to \infty.$
(f) Seja $h(x) = f(x + x_0) - f(x_0)$. Então $h$ é $C^1$, periódica e satisfaz $h(0) = 0$.
Conclua que se $\sum c_k \exp(ik x)$ é a série de Fourier de $f$ então, $\sum c_k \exp(ik x_0) = f(x_0$.
Obs.: esse exercício só demonstra convergência puntual.
Anteriormente nós tinhamos demonstrado convergência uniforme no caso em que $f$ era $C^2$.
domingo, 28 de agosto de 2011
A transformada de Fourier I: motivações e exemplos
A transformada de Fourier é um limite formal da série de Fourier de uma função $L$-periódica no caso em que $L\to \infty$.
Quando uma função têm período $2\pi$ as únicas freqüências em $f(x)$ são números inteiros. Mas quando $f(x)$ não é periódica todas as freqüências são a priori permitidas.
Intuitivamente, como nós vamos ver em breve, a transformada de Fourier "mede" a presença de $\exp(ikx)$ na função $f(x)$.
Existem duas etapas na teoria de integrais de Fourier. A primeira é chamada análise spectral e consiste de calcular a distribuição de freqüências presentes no "sinal" f(x), o segundo passo consiste em reconstruir o sinal $f(x)$ a partir da sua distribuição de freqüencias $\widehat{f}(k)$. Em suma,
Nossa hipótese fundamental daqui em diante é que $f(x)$ é absolutamente integrável na reta real,
$\int_{\mathbb{R}}\vert f(x)\vert dx < \infty.$ A medida que formos precisando de mais hipóteses, vamos restringir a classe de "sinais" f(x) que trabalharemos.
"Teorema." O grau de suavidade de $f(x)$ controla o quão rápido $\widehat{f}(k)$ tende à zero.
Antes de procedermos com a teoria, vamos experimentar com alguns exemplos.
As transformadas fundamentais, eu diria.
Ex. 1: $f(x) = \delta(x) \Rightarrow \widehat{f}(k) = 1.$
Ex. 2: $f(x) = \left\{ \begin{array}{ll} 1, & \vert x\vert < L \\ 0, & \vert x\vert > L \end{array} \right.$
Você pode calcular que $\widehat{f}(k) \propto \sin(k L)/L,$ e a constante de proporcionalidade fica por sua conta.
Ex. 3: $f(x) = \left\{ \begin{array}{ll} exp(-ax), & x \geq 0 \\ 0, & x < 0. \end{array} \right.$ Assumindo $a > 0$ é claro.
Verifique que $\widehat{f}(k) \propto \frac{1}{a + ik}.$
O pólo em $k = i a$ está relacionado com a descontinuidade da função em $x=0$. Por quê? Que tipo de descontinuidades geram pólos?
E.g. 4: $f(x) = \exp(-a \vert x\vert), a > 0.$ A transformada não têm pólos dessa vez! Verifique que $\widehat{f}(k) \propto 1/(a^2 + k^2).$
Ex. 5: E a transformada de uma função constante?
Formalmente falando, a resposta é a função $\delta(k)$. Mas a explanação exige que nos mergulhemos na teoria de funções generalizadas.
Consulte, o livro do Lighthill "Fourier Integrals and Generalized Functions."
Antes de falarmos da teoria de transformadas de Fourier rigorosamente, vamos nos aventurar um pouco mais nos aspectos computacionais.
Mais tarde nós veremos que transformadas de Fourier são bastante úteis no cáculo de funções de Green de operadores lineares.
A próxima pergunta é a seguinte.
Qual é a relação entre $\widehat{f}(k)$ e $\widehat{f'}(k)$? (Se é que elas estão relacionadas.)
Podemos nos perguntar sobre noções semelhantes, como a relação entre a transformada de Fourier e integrais, e a transformada de Fourier e o operador de translação. (Mais sobre esse tópico mais tarde.)
Dada $f(x) = \sum_{k=-\infty}^{\infty} c_k \exp(ikx)$, a derivada $f'$ têm série de Fourier $ \sum_{k=-\infty}^{\infty} ikc_k \exp(ikx)$.
No mundo de integrais de Fourier, essa regra se torna
$f(x) = \frac{1}{2\pi}\int_{-\infty}^{\infty}\widehat{f}(k)\exp(-ikx)dk \Rightarrow \frac{1}{2\pi}\int_{-\infty}^{\infty}\widehat{f}(k)\exp(-ikx)dk$ e da pela fórmula de inversão de Fourier, $\widehat{f'}(k) = ik\widehat{f}(k)$.
Por outro lado, a transformada da integral $F(x) = \int f(x) dx $ é $\widehat{F}(k) = \widehat{f}(k)/ik.$
Outra propriedade computacional interessante da transformada de Fourier, útil em processamento de sinais, é
$f(x-d) = \int_{\mathbb{R}}\exp(-ikd)\widehat{f}(k)\exp(ikx)dx.$
As regras computacionais para a integral de Fourier podem ser resumidas na seguinte lista:
e calcule a transformada da curva normal $f(x) = \exp(-x^2/2)$. (Dica: a transformada é uma curva normal também.)
Quando uma função têm período $2\pi$ as únicas freqüências em $f(x)$ são números inteiros. Mas quando $f(x)$ não é periódica todas as freqüências são a priori permitidas.
Intuitivamente, como nós vamos ver em breve, a transformada de Fourier "mede" a presença de $\exp(ikx)$ na função $f(x)$.
Existem duas etapas na teoria de integrais de Fourier. A primeira é chamada análise spectral e consiste de calcular a distribuição de freqüências presentes no "sinal" f(x), o segundo passo consiste em reconstruir o sinal $f(x)$ a partir da sua distribuição de freqüencias $\widehat{f}(k)$. Em suma,
- $\widehat{f}(k) = \frac{1}{2\pi}\int_{-\infty}^{\infty} f(x)\exp(-ikx) dx,$
- $f(x) = \int_{-\infty}^{\infty} \widehat{f}(k) \exp(ikx) dk.$
Nossa hipótese fundamental daqui em diante é que $f(x)$ é absolutamente integrável na reta real,
$\int_{\mathbb{R}}\vert f(x)\vert dx < \infty.$ A medida que formos precisando de mais hipóteses, vamos restringir a classe de "sinais" f(x) que trabalharemos.
"Teorema." O grau de suavidade de $f(x)$ controla o quão rápido $\widehat{f}(k)$ tende à zero.
Antes de procedermos com a teoria, vamos experimentar com alguns exemplos.
As transformadas fundamentais, eu diria.
Ex. 1: $f(x) = \delta(x) \Rightarrow \widehat{f}(k) = 1.$
Ex. 2: $f(x) = \left\{ \begin{array}{ll} 1, & \vert x\vert < L \\ 0, & \vert x\vert > L \end{array} \right.$
Você pode calcular que $\widehat{f}(k) \propto \sin(k L)/L,$ e a constante de proporcionalidade fica por sua conta.
Ex. 3: $f(x) = \left\{ \begin{array}{ll} exp(-ax), & x \geq 0 \\ 0, & x < 0. \end{array} \right.$ Assumindo $a > 0$ é claro.
Verifique que $\widehat{f}(k) \propto \frac{1}{a + ik}.$
O pólo em $k = i a$ está relacionado com a descontinuidade da função em $x=0$. Por quê? Que tipo de descontinuidades geram pólos?
E.g. 4: $f(x) = \exp(-a \vert x\vert), a > 0.$ A transformada não têm pólos dessa vez! Verifique que $\widehat{f}(k) \propto 1/(a^2 + k^2).$
Ex. 5: E a transformada de uma função constante?
Formalmente falando, a resposta é a função $\delta(k)$. Mas a explanação exige que nos mergulhemos na teoria de funções generalizadas.
Consulte, o livro do Lighthill "Fourier Integrals and Generalized Functions."
Antes de falarmos da teoria de transformadas de Fourier rigorosamente, vamos nos aventurar um pouco mais nos aspectos computacionais.
Mais tarde nós veremos que transformadas de Fourier são bastante úteis no cáculo de funções de Green de operadores lineares.
A próxima pergunta é a seguinte.
Qual é a relação entre $\widehat{f}(k)$ e $\widehat{f'}(k)$? (Se é que elas estão relacionadas.)
Podemos nos perguntar sobre noções semelhantes, como a relação entre a transformada de Fourier e integrais, e a transformada de Fourier e o operador de translação. (Mais sobre esse tópico mais tarde.)
Dada $f(x) = \sum_{k=-\infty}^{\infty} c_k \exp(ikx)$, a derivada $f'$ têm série de Fourier $ \sum_{k=-\infty}^{\infty} ikc_k \exp(ikx)$.
No mundo de integrais de Fourier, essa regra se torna
$f(x) = \frac{1}{2\pi}\int_{-\infty}^{\infty}\widehat{f}(k)\exp(-ikx)dk \Rightarrow \frac{1}{2\pi}\int_{-\infty}^{\infty}\widehat{f}(k)\exp(-ikx)dk$ e da pela fórmula de inversão de Fourier, $\widehat{f'}(k) = ik\widehat{f}(k)$.
Por outro lado, a transformada da integral $F(x) = \int f(x) dx $ é $\widehat{F}(k) = \widehat{f}(k)/ik.$
Outra propriedade computacional interessante da transformada de Fourier, útil em processamento de sinais, é
$f(x-d) = \int_{\mathbb{R}}\exp(-ikd)\widehat{f}(k)\exp(ikx)dx.$
As regras computacionais para a integral de Fourier podem ser resumidas na seguinte lista:
- $f'(x)$ têm transformada $ik \mathbb{f}(k)$ e portanto a transformada da derivada decai mais devagar quando $k\to \infty$. ("As freqências mais altas aumentaram.")
- $\int f(x) dx$ têm transformada $\widehat{\int f(x) dx}(k) = \widehat{f}(k)/ik$, e a transformada decai mais rápido. ("A distribuição de freqüências fica mais concentrada.)
- $f(x - d)$ têm transformada $\exp(-ikd) \widehat{f}(k)$, i.e. "transladando o sinal $f(x)$ muda a fase de $\widehat{f}(k)$."
e calcule a transformada da curva normal $f(x) = \exp(-x^2/2)$. (Dica: a transformada é uma curva normal também.)
sexta-feira, 26 de agosto de 2011
Solução do testinho 1 (função de Dirac periódica)
No testinho 1 eu pedi que vocês calculassem a expansão de Fourier de
$f(x) =
\left\{\begin{array}{ll}
-1, & x\in(-\pi,0) \\
1, & x\in (0,\pi)
\end{array}
\right.$
e extendida periódicamente, i.e. nós recortamos e colamos o gráfico da função em cada intervalo $[(2k-1)\pi,(2k+1)\pi]$ etc.
Em seguida eu pedi que a derivada (no sentido generalizado) de $f(x)$ fosse calculada também. O problema perguntava se a série de Fourier da função original poderia ser calculada a partir da série de Fourier da derivada por integração termo-a-termo.
A série de Fourier de $f(x)$ é $\sum_{\text{k impar}}\frac{4}{\pi k} \sin(kx).$
(A função é ímpar e real.)
O tamanho da descontinuidade da função $f$ no ponto $x = 0$ é 2. O que eu quero dizer é que o pulo têm tamanho + 2 unidades.
No ponto $x = \pi$ o módulo do pulo é o mesmo, mas o sinal muda. E pensando periodicamente você generaliza como o padrão.
As vezes a função $f(x)$ é chamada de função sinal, pois ela retorna o sinal de um número real.
Como a maioria percebeu, $f(x) = 2\theta(x) - 1 \Rightarrow f'(x) = 2\delta(x)$ onde $\theta(x)$ é a função de Heaviside ou a anti-derivada generalizada de $\delta(x)$.
Se não estivéssemos no caso periódico poderíamos parar aqui. Mas a função $f(x)$ é periódica,
e a derivada correta é
$f(x) = \sum_{k\in \mathbb{Z}}c_k \exp(ikx) = \sum_{k=-\infty}^{\infty} 2 (-1)^k \delta(x - k\pi).$
Ou, nós podemos pensar que $\delta(x)$ é o limite de uma sequência de funções do tipo delta, que são $2\pi$ periódicas e que no intervalo fundamental $[-\pi,\pi]$ têm a forma,
$\delta_N(x) =
\left\{
\begin{array}{ll}
-N, & x \in (-\pi,-\pi + 1/2N) \\
N, & x \in (-1/2N,1/2N) \\
-N, & x \in (\pi - 1/2N,\pi)
\end{array}
\right. $
Se você esboçar esseas funções o desenho se parece com uma coleção de caixinhas de altura $N$ (ou -$N$) ao redor de cada $k \pi, k \in \mathbb{Z}$.
Os coeficientes de Fourier de $f'(x)$, que chamaremos aqui $d_k$ são calculados como
$d_k = \lim_{N\to\infty}\frac{1}{2\pi}\int_{-\pi}^{\pi} \delta_N(x) \exp(-ixk) dx.$
Escrevendo $f'(x) = \sum_{k\in \mathbb{Z}} d_k \exp(ikx)$ e integrando termo-a-termo na série infinita nos recuperaremos $\sum c_k exp(ikx)$.
$f(x) =
\left\{\begin{array}{ll}
-1, & x\in(-\pi,0) \\
1, & x\in (0,\pi)
\end{array}
\right.$
e extendida periódicamente, i.e. nós recortamos e colamos o gráfico da função em cada intervalo $[(2k-1)\pi,(2k+1)\pi]$ etc.
Em seguida eu pedi que a derivada (no sentido generalizado) de $f(x)$ fosse calculada também. O problema perguntava se a série de Fourier da função original poderia ser calculada a partir da série de Fourier da derivada por integração termo-a-termo.
A série de Fourier de $f(x)$ é $\sum_{\text{k impar}}\frac{4}{\pi k} \sin(kx).$
(A função é ímpar e real.)
O tamanho da descontinuidade da função $f$ no ponto $x = 0$ é 2. O que eu quero dizer é que o pulo têm tamanho + 2 unidades.
No ponto $x = \pi$ o módulo do pulo é o mesmo, mas o sinal muda. E pensando periodicamente você generaliza como o padrão.
As vezes a função $f(x)$ é chamada de função sinal, pois ela retorna o sinal de um número real.
Como a maioria percebeu, $f(x) = 2\theta(x) - 1 \Rightarrow f'(x) = 2\delta(x)$ onde $\theta(x)$ é a função de Heaviside ou a anti-derivada generalizada de $\delta(x)$.
Se não estivéssemos no caso periódico poderíamos parar aqui. Mas a função $f(x)$ é periódica,
e a derivada correta é
$f(x) = \sum_{k\in \mathbb{Z}}c_k \exp(ikx) = \sum_{k=-\infty}^{\infty} 2 (-1)^k \delta(x - k\pi).$
Ou, nós podemos pensar que $\delta(x)$ é o limite de uma sequência de funções do tipo delta, que são $2\pi$ periódicas e que no intervalo fundamental $[-\pi,\pi]$ têm a forma,
$\delta_N(x) =
\left\{
\begin{array}{ll}
-N, & x \in (-\pi,-\pi + 1/2N) \\
N, & x \in (-1/2N,1/2N) \\
-N, & x \in (\pi - 1/2N,\pi)
\end{array}
\right. $
Se você esboçar esseas funções o desenho se parece com uma coleção de caixinhas de altura $N$ (ou -$N$) ao redor de cada $k \pi, k \in \mathbb{Z}$.
Os coeficientes de Fourier de $f'(x)$, que chamaremos aqui $d_k$ são calculados como
$d_k = \lim_{N\to\infty}\frac{1}{2\pi}\int_{-\pi}^{\pi} \delta_N(x) \exp(-ixk) dx.$
Escrevendo $f'(x) = \sum_{k\in \mathbb{Z}} d_k \exp(ikx)$ e integrando termo-a-termo na série infinita nos recuperaremos $\sum c_k exp(ikx)$.
Derivação da equação da corda
Seguindo o Mark Embree,
eu vou postar uma diagrama aqui que exemplifica a situação típica da perturbação de uma corda fina carregada com miçangas.
Em geral essa seria a situação típica resultante da perturbação da corda por uma força externa vertical aplicada à corda que estava inicialmente em repouso.
A massas $m_i$ (denotadas pelos pontões gordos) podem se deslocar horizontalmente, e verticalmente.
Além do mais, os ângulos $\phi_i$'s podem ser determinados através de formulas trigonométricas (exercício).
Por exemplo,
Supondo que a deformação entre os segmentos de corda entre quaisquer duas massas seja pequena, a interação entre quaisquer duas massas se dá através da lei de Hook. Nós comentaremos mais à respeito da deformação da corda sob efeito de uma perturbação externa mais tarde.
Se a perturbação for suficientemente pequena, os livros em geral assumem que a tensão na corda é aproximadamente constante.
Em física, supõe-se em geral que um fio de material elástico se comporta como uma mola linear, i.e. a resistência à obedece a lei de Hook.
Suponha também que uma certa tensão $\tau$ foi aplicada à corda.
Dessa forma, a força sofrida pela massa $m_j$ no modelo é (approximadamente)
$$\tau (\cos(\phi_j) - \cos(\phi_{j-1}), \sin(\phi_j) - \sin(\phi_{j-1})).$$
Os ângulos $\phi_j$ ficam determinados pelos deslocamentos através de fórmulas trigonométricas simples involvendo os deslocamentos horizontais e verticais,
$\cos(\phi_j) = \frac{l_j + x_{j+1} - x_j}{\sqrt{(l_j + x_{j+1} - x_j)^2 + (y_{j+1} - y_j)^2}}.$
Se nós assumirmos que $l_j \gg \vert x_{j+1} - x_j\vert , l_j \gg \vert y_{j+1} - y_j\vert $ então nós temos que,
$\cos(\phi_j) \approx 1$ e $\sin(\phi_j) \approx \frac{y_{j+1} - y_j}{l_j}.$
Intuitivamente, se $l_j = h,\forall j$ então $\vert x_{j+1} - x_j\vert = O(h^2)$ etc.
Como exercício derive as outras fórmulas e aproximações necessárias para o cálculo da força de Hooke atuando em cada massa, ou miçanga.
No final, se nós fizermos os cálculos corretamente, em primeira ordem nós podemos assumir que a componente da força restauradora é maioritariamente vertical.
Portanto nós podemos utilizar o seguinte diagrama de dislocamento vertical da corda. Daqui em diante, para evitar confusão eu vou denotar os pontos no eixo horizontal onde as massas $m_i$ estavam inicialmente em repouso por $x_j$ e o deslocamento vertical dessas massas por $u(x_j) = u_j$. devido A força de tensão vertical é denotada por $F$. (Com os seus dedos você toca o violão de uma corda. )
Obs.: No diagrama a corda sofre uma dilatação. O comprimento da corda dilatada é fácil de calcular,
$l' = \sqrt{h^2 + u_1}^2 + \sqrt{h^2 + (u_1 - u_2)^2} + \dots \sqrt{h^2 + (u_N - u_{N-1})^2} + + \sqrt{h^2 + u_N^2}.$
Uma expansão em séries de Taylor para $\sqrt{1 + \epsilon}$ nos dá nesse caso,
$l' = h(1 + \frac{1}{2}\frac{u_1^2}{h^2} + O(2)) + h(1 + \frac{1}{2}\frac{(u_1 - u_2)^2}{h^2} + \dots + O(2)) + h(1 + \frac{1}{2}\frac{(u_{N} - u_{N-1})^2}{h^2} + O(2)) + h(1 + \frac{1}{2}\frac{u_1^2}{h^2} + O(2)).$
Agora os termos $\Delta u_j = u_j - u_{j-1}$ são todos da ordem $O(h^2)$ de acordo com a nossa hipótese.
O tamanho inicial da corda é $l \approx h N$ e $h = O(1/N)$. Portanto,
$l' = l + h\sum_j \frac{\Delta u_j^2}{h^2} + O(h^3)$. O segundo termo no lado direito é uma soma de $N$ termos de ordem $h^2$ e portanto nós podemos estimar a soma no lado direito como
$l'= l + O(h^2)$.
A variação em comprimento $\Delta l$ e da ordem de $h$.
Considere agora as equações de movimento de cada $m_i$.
Nossa hipótese simplificadora é que $m_i = m$ e que a distância entre elas é fixa.
No limite quando $h,m \to 0$ nós vamos considerar o caso $m/h \to \text{const.}$, i.e. a distribuição linear de massa tende tende à uma constante.
As equações de movimento são:
$\left\{
\begin{array}{ll}
m \ddot{u}_1 = & -F\frac{u_1}{h} + F\frac{u_2 - u_1}{h}, \\
m \ddot{u}_2 = & -F\frac{u_2 - u_1}{h} + F\frac{u_3 - u_2}{h},\\
\vdots & \vdots \\
m \ddot{u}_N = & -F\frac{u_N - u_{N-1}}{h} + F\frac{u_N }{h}.
\end{array}
\right. $
Dividindo ambos os lados por $h$ (e a razão vai ficar clara logo),
nós obteremos o sistema linear de segunda ordem da forma,
$\frac{m}{h} \mathbf{u} =\mathbf{ -K u},$
onde $\mathbf{u} = (u_1,u_2,\dots,u_N)$ e
$K = \frac{-F}{h^2}
\left(
\begin{array}{cccccc}
2 & -1 & 0 & 0 & 0 & \dots \\
-1 & 2 & -1 & 0 & \dots & \dots\\
0 & -1 & 2 & -1 & 0 & \dots \\
\vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\
0 & \dots & -1& -2 & -1 & 0 \\
0 & \dots & 0 & -1& -2 & -1 \\
0 & 0 & \dots & \dots & -1 & 2 \\
\end{array}\right).$
A matriz tridiagonal $\mathbf{K}$ é extremamente importante em análise númerica, e está relacionada com um método de discretização chamado diferenças finitas. A matriz $K$ é quadrada e têm dimensão $N$. Quando $h\to 0$ e o número de miçangas tende ao infinito, nós vamos ter no limite um sistema linear de "dimensão infinita."
Para concluir a nossa estória, considere uma malha no intervalo $[0, l]$. Nós estamos amostrando uma certa função $u(x,t)$ em certos pontos $x_k = 0 + kh$, igualmente espaçados.
Ponto-a-ponto, nos nós da malha, nós temos que
$\ddot{u}(x_j,t) = -F\frac{u(x_{j+1},t) - 2 u(x_j,t) + u(x_{j-1},t)}{h^2},$
e um simples argumento involvendo séries de Taylor vai convence-lo de que a razão no lado direito é de fato uma aproximação para
$u_{xx}(x_j,t)$ com erro de ordem $O(h)$.
Portanto,
$\frac{m}{h}u_{tt}(x_j,t) = F u_{xx}(x_j,t) + O(h). $
No limite $h,m\to 0$, $m/h \to \rho > 0$ e nós recuperamos a equação da corda. A velocidade ao quadrado $c^2$ que aparece na equação da corda é a razão entre $F/\rho$.
eu vou postar uma diagrama aqui que exemplifica a situação típica da perturbação de uma corda fina carregada com miçangas.
 |
| Diagrama 1. |
A massas $m_i$ (denotadas pelos pontões gordos) podem se deslocar horizontalmente, e verticalmente.
Além do mais, os ângulos $\phi_i$'s podem ser determinados através de formulas trigonométricas (exercício).
Por exemplo,
Supondo que a deformação entre os segmentos de corda entre quaisquer duas massas seja pequena, a interação entre quaisquer duas massas se dá através da lei de Hook. Nós comentaremos mais à respeito da deformação da corda sob efeito de uma perturbação externa mais tarde.
Se a perturbação for suficientemente pequena, os livros em geral assumem que a tensão na corda é aproximadamente constante.
Em física, supõe-se em geral que um fio de material elástico se comporta como uma mola linear, i.e. a resistência à obedece a lei de Hook.
Suponha também que uma certa tensão $\tau$ foi aplicada à corda.
Dessa forma, a força sofrida pela massa $m_j$ no modelo é (approximadamente)
$$\tau (\cos(\phi_j) - \cos(\phi_{j-1}), \sin(\phi_j) - \sin(\phi_{j-1})).$$
Os ângulos $\phi_j$ ficam determinados pelos deslocamentos através de fórmulas trigonométricas simples involvendo os deslocamentos horizontais e verticais,
$\cos(\phi_j) = \frac{l_j + x_{j+1} - x_j}{\sqrt{(l_j + x_{j+1} - x_j)^2 + (y_{j+1} - y_j)^2}}.$
Se nós assumirmos que $l_j \gg \vert x_{j+1} - x_j\vert , l_j \gg \vert y_{j+1} - y_j\vert $ então nós temos que,
$\cos(\phi_j) \approx 1$ e $\sin(\phi_j) \approx \frac{y_{j+1} - y_j}{l_j}.$
Intuitivamente, se $l_j = h,\forall j$ então $\vert x_{j+1} - x_j\vert = O(h^2)$ etc.
Como exercício derive as outras fórmulas e aproximações necessárias para o cálculo da força de Hooke atuando em cada massa, ou miçanga.
No final, se nós fizermos os cálculos corretamente, em primeira ordem nós podemos assumir que a componente da força restauradora é maioritariamente vertical.
Portanto nós podemos utilizar o seguinte diagrama de dislocamento vertical da corda. Daqui em diante, para evitar confusão eu vou denotar os pontos no eixo horizontal onde as massas $m_i$ estavam inicialmente em repouso por $x_j$ e o deslocamento vertical dessas massas por $u(x_j) = u_j$. devido A força de tensão vertical é denotada por $F$. (Com os seus dedos você toca o violão de uma corda. )
Obs.: No diagrama a corda sofre uma dilatação. O comprimento da corda dilatada é fácil de calcular,
 |
| Diagrama 2. |
Uma expansão em séries de Taylor para $\sqrt{1 + \epsilon}$ nos dá nesse caso,
$l' = h(1 + \frac{1}{2}\frac{u_1^2}{h^2} + O(2)) + h(1 + \frac{1}{2}\frac{(u_1 - u_2)^2}{h^2} + \dots + O(2)) + h(1 + \frac{1}{2}\frac{(u_{N} - u_{N-1})^2}{h^2} + O(2)) + h(1 + \frac{1}{2}\frac{u_1^2}{h^2} + O(2)).$
Agora os termos $\Delta u_j = u_j - u_{j-1}$ são todos da ordem $O(h^2)$ de acordo com a nossa hipótese.
O tamanho inicial da corda é $l \approx h N$ e $h = O(1/N)$. Portanto,
$l' = l + h\sum_j \frac{\Delta u_j^2}{h^2} + O(h^3)$. O segundo termo no lado direito é uma soma de $N$ termos de ordem $h^2$ e portanto nós podemos estimar a soma no lado direito como
$l'= l + O(h^2)$.
A variação em comprimento $\Delta l$ e da ordem de $h$.
Considere agora as equações de movimento de cada $m_i$.
Nossa hipótese simplificadora é que $m_i = m$ e que a distância entre elas é fixa.
No limite quando $h,m \to 0$ nós vamos considerar o caso $m/h \to \text{const.}$, i.e. a distribuição linear de massa tende tende à uma constante.
As equações de movimento são:
$\left\{
\begin{array}{ll}
m \ddot{u}_1 = & -F\frac{u_1}{h} + F\frac{u_2 - u_1}{h}, \\
m \ddot{u}_2 = & -F\frac{u_2 - u_1}{h} + F\frac{u_3 - u_2}{h},\\
\vdots & \vdots \\
m \ddot{u}_N = & -F\frac{u_N - u_{N-1}}{h} + F\frac{u_N }{h}.
\end{array}
\right. $
Dividindo ambos os lados por $h$ (e a razão vai ficar clara logo),
nós obteremos o sistema linear de segunda ordem da forma,
$\frac{m}{h} \mathbf{u} =\mathbf{ -K u},$
onde $\mathbf{u} = (u_1,u_2,\dots,u_N)$ e
$K = \frac{-F}{h^2}
\left(
\begin{array}{cccccc}
2 & -1 & 0 & 0 & 0 & \dots \\
-1 & 2 & -1 & 0 & \dots & \dots\\
0 & -1 & 2 & -1 & 0 & \dots \\
\vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\
0 & \dots & -1& -2 & -1 & 0 \\
0 & \dots & 0 & -1& -2 & -1 \\
0 & 0 & \dots & \dots & -1 & 2 \\
\end{array}\right).$
A matriz tridiagonal $\mathbf{K}$ é extremamente importante em análise númerica, e está relacionada com um método de discretização chamado diferenças finitas. A matriz $K$ é quadrada e têm dimensão $N$. Quando $h\to 0$ e o número de miçangas tende ao infinito, nós vamos ter no limite um sistema linear de "dimensão infinita."
Para concluir a nossa estória, considere uma malha no intervalo $[0, l]$. Nós estamos amostrando uma certa função $u(x,t)$ em certos pontos $x_k = 0 + kh$, igualmente espaçados.
Ponto-a-ponto, nos nós da malha, nós temos que
$\ddot{u}(x_j,t) = -F\frac{u(x_{j+1},t) - 2 u(x_j,t) + u(x_{j-1},t)}{h^2},$
e um simples argumento involvendo séries de Taylor vai convence-lo de que a razão no lado direito é de fato uma aproximação para
$u_{xx}(x_j,t)$ com erro de ordem $O(h)$.
Portanto,
$\frac{m}{h}u_{tt}(x_j,t) = F u_{xx}(x_j,t) + O(h). $
No limite $h,m\to 0$, $m/h \to \rho > 0$ e nós recuperamos a equação da corda. A velocidade ao quadrado $c^2$ que aparece na equação da corda é a razão entre $F/\rho$.
segunda-feira, 22 de agosto de 2011
O modelo de miçangas na vida real.
A fotos abaixo são cortesia de Mark Embree da Rice University de Houson, no estado do Texas.
 |
| Para ler mais sobre o modelo e os experimentos realizados por Mark e o seus estudantes, explore http://www.caam.rice.edu/~beads/. |
quinta-feira, 18 de agosto de 2011
Funções de Green (ou função causal da influência de um distúrbio no instante $a$ no ponto $x$.)
Princípio de linearidade ou superposição.
Seja $A$ um operador linear e sejam $\phi_1,\phi_2$ soluções da equação $Au = g_1$ e $Au = g_2$ respectivamente.
Então $(\phi_1 + \phi_2)$ é solução da equação $Au = \phi_1 + \phi_2$.
Aqui $A$ pode ser uma equação diferencial ordinária, ou uma equação diferencial parcial, e o espaço de funções onde o operador atua satisfaz condições de fronteira apropriadas.
A solução $u$ de uma equação linear do tipo $Au = g$ representa a resposta do sistema ao distúrbio (externo) $g$.
Superposição nos permite considerar os efeitos de perturbações individualmente.
Portanto nós vamos considerar primeiro perturbações que são puntuais. Integração (na forma de convolução) vai nos permitir considerar perturbações mais gerais.
Definição. Uma seqüência de funções $(\delta_N)$ do tipo $\delta$ é uma seqüência de funções positivas com suporte compacto concentrado na origem $x = 0$, e que satisfaz as seguintes propriedades
$\int_{\mathbb{R}} \delta_N dx = 1,$ e
$\overline{ \text{suporte}(\delta_N) } = \overline{ \{ x\in\mathbb{R}: \delta_N(x) \neq 0 \} } \to \{0\}$ quando $N\to \infty$.
O exemplo que nós vamos considerar aqui é a sequência de funções
$\delta_N(x) = \left\{
\begin{array}{ll}
N, & \vert x\vert \leq 1/2N \\
0, & \vert x\vert > 1/2N.
\end{array}
\right.$
Portanto $\delta_N(x)$ não precisa nem ser contínua. Antes de provarmos uma propriedade fundamental das seqüências do tipo delta, nós demonstraremos o seguinte fato auxiliar.
Lema. Se $g(x)$ é contínua em $I = [a,b]$ e $h(x)$ é integrável e positiva em $I = [a,b]$ então
$\exists c \in [a,b]$ t.q. $g(c) = \frac{1}{A}\int_{a}^{b}g(x)h(x)dx,$
onde $A = \int_I h(x) dx.$
E se $A = 0$? Nós vamos assumir primeiro que $A \neq 0$.
Prova. Sejam $m,M$ o máximo e mínimo (resp.) de $g(x)$ no intervalo $I$, i.e. $m \leq g(x) \leq M, \forall x\in I$. Como consequência, $ m \int_{a}^{b}h(x)dx \leq \int_{a}^{b}g(x)h(x) dx \leq
M \int_{a}^{b} h(x)dx$, ou ainda que $m \leq \frac{1}{A}\int_{a}^{b}g(x)h(x) dx \leq M$ assumindo que $A\neq 0$.
A continuidade de $g(x)$ implica que as quotas $m,M$ pertencem a imagem de $g(x)$. Além disso, pelo teorema do valor intermediário, qualquer valor entre $m,M$ é alcançado pela função $g(x)$.
(O intervalo $[m,M]$ está contido na imagem de $g(x)$.)
Isso conclui a demonstração do lema. Q.E.D.
Prove que se $A = 0$, sob a hipótese que $h(x)$ é positiva e integrável, então $h(x)$ é zero.
Integrabilidade aqui é no sentido de Riemann. Acho que o problema é válido para funções integráveis no sentido de Lebesgue.
Será que nós podemos provar o lema se $\phi(x)$ puder tomar valores negativos, mas a integral de $\phi(x)$ é positiva? Prove ou ache um contra-exemplo. (Exercício.)
De volta ao mundo dos mortais, nós podemos provar o seguinte
Proposição. Se $g(x)$ for contínua então e $(\delta_N(x)$ é uma função do tipo delta,
$$\lim_{N\to \infty} \int_{\mathbb{R}}g(x) \delta_N(x) dx = g(0).$$
Em análise funcional nós diríamos que a seqüência $(\delta_N(x))$ converge fracamente.
Pense que o mapa $g(x) \mapsto \int_{\mathbb{R}}(\underline{\bullet})\delta_N(x) dx$ define um funcional no espaço de funções contínuas. O limite desse funcional é o que os físicos chamam de função delta (de Dirac), ou $\delta(x)$.
Formalmente $\delta[g(x)] = g(0)$.
A prova da proposição é uma aplicação direta da nossa versão acima do teorema do valor médio para integrais.
Uma conseqüência básica dessas idéias é a idéia de função de Green causal.
Definição. A função de Green (causal) $G(x;a)$ é a solução do problema de Cauchy
$\left\{
\begin{array}{l}
\frac{d y}{dx} - f(x)y = \delta(x - a) , \\
y(x_0) = 0 , a > x_0.
\end{array}
\right.$
Em geral nós iniciamos o cronômetro em $x = 0$.
Como interpretar essa última equação propriamente? Mais precisamente, como interpretar $G(x;a)$ rigorosamente?
Seja $y_N(x;a)$ a solução do problema de Cauchy
$\left\{
\begin{array}{l}
\frac{dy}{dx} - f(x)y = \delta_N(x-a),\\
y(0) = 0
\end{array}
\right.$
onde $(\delta_N(x-a))$ é uma seqüência de funções do tipo delta concentrada perto no ponto $a$.
Definição. $G(x;a) = \lim_{N \to \infty} y_N(x)$.
Nós vamos ver que esse limite não depende da escolha da seqüência do tipo delta.
Para mostrar que a função $G(x;a)$ é bem definida nós vamos retroceder um pouco e relembrar algumas formulas do curso de Cálculo 4.
A solução de uma equação linear não homogênea é da forma $y_N(x) = c(x) y_0(x)$ onde $y_0$ é a solução da equação homogênea associada.
A função $c(x)$ é obtida substituindo o "chute" $c(x)y_0(x)$ na equação não homogênea.
A solução geral fica,
$y_N(x) = \int_0^x \exp(\int_s^x f(t) dt) \delta_N(s) ds.$
Proposição. A função de Green $G(x;a)$ é dada pela fórmula
$G(x;a) =
\left\{\begin{array}{ll}
0, & x < a \\
\exp(\int_a^x f(t) dt) & x \geq a.
\end{array}
\right.$
A prova depende da propriedade fundamental das seqüências do tipo delta. Da fórmula fórmula nós inferimos que $G(x;a)$ é descontínua em $x=a$. A resposta do sistema é unitária no instante da perturbação $\delta(x-a)$.
Como exercício eu pedi que vocês calculasses a função de Green do seguinte problema de Cauchy para a EDO de segunda ordem (equações de Newton) do pêndulo simples:
$\left\{
\begin{array}{l}
\frac{d^2 x}{dt^2} = \frac{-k}{m}x + \delta(x-a) \\
x(0) = \dot{x}(0) = 0.
\end{array}
\right.$
Isso descreve a equação de um pêndulo inicialmente em repouso e que sofre uma pancada instantânea no instante $t = a$.
Em resumo, o formalismo de funções é bastante conveniente quando calcularmos soluções numéricas e ou analíticas de EDP's lineares.
Seja $A$ um operador linear e sejam $\phi_1,\phi_2$ soluções da equação $Au = g_1$ e $Au = g_2$ respectivamente.
Então $(\phi_1 + \phi_2)$ é solução da equação $Au = \phi_1 + \phi_2$.
Aqui $A$ pode ser uma equação diferencial ordinária, ou uma equação diferencial parcial, e o espaço de funções onde o operador atua satisfaz condições de fronteira apropriadas.
A solução $u$ de uma equação linear do tipo $Au = g$ representa a resposta do sistema ao distúrbio (externo) $g$.
Superposição nos permite considerar os efeitos de perturbações individualmente.
Portanto nós vamos considerar primeiro perturbações que são puntuais. Integração (na forma de convolução) vai nos permitir considerar perturbações mais gerais.
Definição. Uma seqüência de funções $(\delta_N)$ do tipo $\delta$ é uma seqüência de funções positivas com suporte compacto concentrado na origem $x = 0$, e que satisfaz as seguintes propriedades
$\int_{\mathbb{R}} \delta_N dx = 1,$ e
$\overline{ \text{suporte}(\delta_N) } = \overline{ \{ x\in\mathbb{R}: \delta_N(x) \neq 0 \} } \to \{0\}$ quando $N\to \infty$.
O exemplo que nós vamos considerar aqui é a sequência de funções
$\delta_N(x) = \left\{
\begin{array}{ll}
N, & \vert x\vert \leq 1/2N \\
0, & \vert x\vert > 1/2N.
\end{array}
\right.$
Portanto $\delta_N(x)$ não precisa nem ser contínua. Antes de provarmos uma propriedade fundamental das seqüências do tipo delta, nós demonstraremos o seguinte fato auxiliar.
Lema. Se $g(x)$ é contínua em $I = [a,b]$ e $h(x)$ é integrável e positiva em $I = [a,b]$ então
$\exists c \in [a,b]$ t.q. $g(c) = \frac{1}{A}\int_{a}^{b}g(x)h(x)dx,$
onde $A = \int_I h(x) dx.$
E se $A = 0$? Nós vamos assumir primeiro que $A \neq 0$.
Prova. Sejam $m,M$ o máximo e mínimo (resp.) de $g(x)$ no intervalo $I$, i.e. $m \leq g(x) \leq M, \forall x\in I$. Como consequência, $ m \int_{a}^{b}h(x)dx \leq \int_{a}^{b}g(x)h(x) dx \leq
M \int_{a}^{b} h(x)dx$, ou ainda que $m \leq \frac{1}{A}\int_{a}^{b}g(x)h(x) dx \leq M$ assumindo que $A\neq 0$.
A continuidade de $g(x)$ implica que as quotas $m,M$ pertencem a imagem de $g(x)$. Além disso, pelo teorema do valor intermediário, qualquer valor entre $m,M$ é alcançado pela função $g(x)$.
(O intervalo $[m,M]$ está contido na imagem de $g(x)$.)
Isso conclui a demonstração do lema. Q.E.D.
Prove que se $A = 0$, sob a hipótese que $h(x)$ é positiva e integrável, então $h(x)$ é zero.
Integrabilidade aqui é no sentido de Riemann. Acho que o problema é válido para funções integráveis no sentido de Lebesgue.
Será que nós podemos provar o lema se $\phi(x)$ puder tomar valores negativos, mas a integral de $\phi(x)$ é positiva? Prove ou ache um contra-exemplo. (Exercício.)
De volta ao mundo dos mortais, nós podemos provar o seguinte
Proposição. Se $g(x)$ for contínua então e $(\delta_N(x)$ é uma função do tipo delta,
$$\lim_{N\to \infty} \int_{\mathbb{R}}g(x) \delta_N(x) dx = g(0).$$
Em análise funcional nós diríamos que a seqüência $(\delta_N(x))$ converge fracamente.
Pense que o mapa $g(x) \mapsto \int_{\mathbb{R}}(\underline{\bullet})\delta_N(x) dx$ define um funcional no espaço de funções contínuas. O limite desse funcional é o que os físicos chamam de função delta (de Dirac), ou $\delta(x)$.
Formalmente $\delta[g(x)] = g(0)$.
A prova da proposição é uma aplicação direta da nossa versão acima do teorema do valor médio para integrais.
Uma conseqüência básica dessas idéias é a idéia de função de Green causal.
Definição. A função de Green (causal) $G(x;a)$ é a solução do problema de Cauchy
$\left\{
\begin{array}{l}
\frac{d y}{dx} - f(x)y = \delta(x - a) , \\
y(x_0) = 0 , a > x_0.
\end{array}
\right.$
Em geral nós iniciamos o cronômetro em $x = 0$.
Como interpretar essa última equação propriamente? Mais precisamente, como interpretar $G(x;a)$ rigorosamente?
Seja $y_N(x;a)$ a solução do problema de Cauchy
$\left\{
\begin{array}{l}
\frac{dy}{dx} - f(x)y = \delta_N(x-a),\\
y(0) = 0
\end{array}
\right.$
Definição. $G(x;a) = \lim_{N \to \infty} y_N(x)$.
Nós vamos ver que esse limite não depende da escolha da seqüência do tipo delta.
Para mostrar que a função $G(x;a)$ é bem definida nós vamos retroceder um pouco e relembrar algumas formulas do curso de Cálculo 4.
A solução de uma equação linear não homogênea é da forma $y_N(x) = c(x) y_0(x)$ onde $y_0$ é a solução da equação homogênea associada.
A função $c(x)$ é obtida substituindo o "chute" $c(x)y_0(x)$ na equação não homogênea.
A solução geral fica,
$y_N(x) = \int_0^x \exp(\int_s^x f(t) dt) \delta_N(s) ds.$
Proposição. A função de Green $G(x;a)$ é dada pela fórmula
$G(x;a) =
\left\{\begin{array}{ll}
0, & x < a \\
\exp(\int_a^x f(t) dt) & x \geq a.
\end{array}
\right.$
A prova depende da propriedade fundamental das seqüências do tipo delta. Da fórmula fórmula nós inferimos que $G(x;a)$ é descontínua em $x=a$. A resposta do sistema é unitária no instante da perturbação $\delta(x-a)$.
Como exercício eu pedi que vocês calculasses a função de Green do seguinte problema de Cauchy para a EDO de segunda ordem (equações de Newton) do pêndulo simples:
$\left\{
\begin{array}{l}
\frac{d^2 x}{dt^2} = \frac{-k}{m}x + \delta(x-a) \\
x(0) = \dot{x}(0) = 0.
\end{array}
\right.$
Isso descreve a equação de um pêndulo inicialmente em repouso e que sofre uma pancada instantânea no instante $t = a$.
Em resumo, o formalismo de funções é bastante conveniente quando calcularmos soluções numéricas e ou analíticas de EDP's lineares.
quarta-feira, 17 de agosto de 2011
seminário q.t.p. para alunos de graduação
Mensagem do diretor do DMAT segue:
seminario q.t.p., para não terminar em pizza!
 Reply
Reply
seminario q.t.p., para não terminar em pizza!
Inbox X
Inbox
 Reply
Reply
| show details 8:48 PM (1 minute ago) |
prezados colegas principais,
thomas e eu estamos organizando o seminário de divulgação
"seminario q.t.p."
dedicado especialmente aos nossos alunos, os mais maduros e os menos maduros,
(e seus professores também serão muito bem-vindos). será (ou
pretendemos que seja)
um seminário informal e descontraído -até divertido- onde um pesquisador
explicará os problemas da sua área e tentará passar algumas ideias.
este seminário será também uma ótima oportunidade para os professores
do dmat divulgar sua pesquisa para os alunos (achamos que muitos
não sabem muito bem o que fazemos.....). assim propostas de palestras, temas,
palestrantes são bem-vindos. se vs. querem "palestrar" melhor ainda!
contamos com sua ajuda, colaboração.... e suas palestras.
o seminário terminará em pizza, o que explica o nome do seminário,
(completem o significado das siglas) financiada pelo dmat, com uma
pequena confraternização.
a primeira palestra será na proxima quarta, as 17h30min. será
ministrada pela nossa ex-aluna Bianca Santoro. O tema é de primeira:
Fluxos de Ricci para iniciantes. por favor, não esqueçam de divulgar!
Um abraço
Thomas e Lorenzo
thomas e eu estamos organizando o seminário de divulgação
"seminario q.t.p."
dedicado especialmente aos nossos alunos, os mais maduros e os menos maduros,
(e seus professores também serão muito bem-vindos). será (ou
pretendemos que seja)
um seminário informal e descontraído -até divertido- onde um pesquisador
explicará os problemas da sua área e tentará passar algumas ideias.
este seminário será também uma ótima oportunidade para os professores
do dmat divulgar sua pesquisa para os alunos (achamos que muitos
não sabem muito bem o que fazemos.....). assim propostas de palestras, temas,
palestrantes são bem-vindos. se vs. querem "palestrar" melhor ainda!
contamos com sua ajuda, colaboração.... e suas palestras.
o seminário terminará em pizza, o que explica o nome do seminário,
(completem o significado das siglas) financiada pelo dmat, com uma
pequena confraternização.
a primeira palestra será na proxima quarta, as 17h30min. será
ministrada pela nossa ex-aluna Bianca Santoro. O tema é de primeira:
Fluxos de Ricci para iniciantes. por favor, não esqueçam de divulgar!
Um abraço
Thomas e Lorenzo
domingo, 14 de agosto de 2011
O fenômeno de Gibbs
A série de Fourier de uma função descontínua $\phi(x)$ periódica não pode convergir uniformemente para a função, mas ela pode convergir ponto-à-ponto.
Nos pontos de descontinuidade a seqüência dos gráficos das somas parciais $S_N(x) = a_0 + \sum_{k=1}^N (a_k \cos(kx) + b_k \sin(kx))$ converge para uma curva que é uma superposição do gráfico da função descontínua original e segmentos e segmentos verticais que excedem o tamanho do salto $\delta$ da função na descontinuidade por aproximadamente $0.08 \times \delta$ acima e abaixo do gráfico original.
Ilustremos o fenômeno. Considere a função onda quadrada com saltos de $\pi/2$ nos pontos de descontinuidade. Isto é, quando $x = 0, \pm \pi, \dots $ etc. a função salta de $-\pi/4$ para $\pi/4$.
Se a função fosse contínua a seqüência $S_N(\pi/N)$ convergiria para $\phi(0) = 0.$
(Em geral, nos pontos de descontinuidade $p$ de $\phi(x)$, a série de Fourier converge para a média
$\lim_{\epsilon \to 0} \frac{\phi(p + \epsilon^2) + \phi(p - \epsilon^2)}{2}.$ )
É fácil calcular a $S_N(x)$ para a onda quadrada,
$$2\times S_N(x) = \sin(x) + \frac{1}{3}\sin(3x) + \frac{1}{5}\sin(5x) + \dots + \frac{1}{N-1} \sin ((N-1)x),$$
onde o último termo só é não zero se $N$ for par.
Nós temos
$2\times S_N(\pi/N) = \sin(\pi/N) + \frac{1}{3}\sin(3\pi/N) + \frac{1}{5}\sin(5\pi/N) + \dots + \frac{1}{N} \sin ((N-1) \pi/N), $
$ =\times( 0 + \frac{\pi}{N}\frac{\sin(\frac{\pi}{N})}{\frac{\pi}{N}} + \frac{\pi}{N}\frac{\sin(\frac{3\pi}{N})}{\frac{3\pi}{N}} +
\frac{\pi}{N}\frac{\sin(\frac{5\pi}{N})}{\frac{5\pi}{N}} + \dots +
\frac{\pi}{N}\frac{\sin(\frac{(N-1)\pi}{N})}{\frac{\pi}{N}}).$
Tomando o limite $N \to \infty$ a soma parcial na última linha se torna,
$\to \int_0^{\pi} \frac{\sin(x)}{x} dx = 1.85194 \Rightarrow S_N(\pi/N) \approx 0.5 \times 1.85194 \approx \pi/4 + 0.08 \times \pi/2 . $
(Nós tínhamos uma soma de Riemann no intervalo de $[0,\pi]$, onde na aproximação por retângulos nós dividimos o intervalo em $k$ ou $k-1$ subintervalos, dependendo se $N=2k$ ou $2k-1$ e a altura de cada sub-retângulo era o valor da função no meio dos subintervalos.)
A função $\text{sinc}(x) = \sin(x)/x$ é bem conhecida na literatura, e é continua no intervalo $[0,\pi]$.
Nos pontos de descontinuidade a seqüência dos gráficos das somas parciais $S_N(x) = a_0 + \sum_{k=1}^N (a_k \cos(kx) + b_k \sin(kx))$ converge para uma curva que é uma superposição do gráfico da função descontínua original e segmentos e segmentos verticais que excedem o tamanho do salto $\delta$ da função na descontinuidade por aproximadamente $0.08 \times \delta$ acima e abaixo do gráfico original.
Ilustremos o fenômeno. Considere a função onda quadrada com saltos de $\pi/2$ nos pontos de descontinuidade. Isto é, quando $x = 0, \pm \pi, \dots $ etc. a função salta de $-\pi/4$ para $\pi/4$.
Se a função fosse contínua a seqüência $S_N(\pi/N)$ convergiria para $\phi(0) = 0.$
(Em geral, nos pontos de descontinuidade $p$ de $\phi(x)$, a série de Fourier converge para a média
$\lim_{\epsilon \to 0} \frac{\phi(p + \epsilon^2) + \phi(p - \epsilon^2)}{2}.$ )
É fácil calcular a $S_N(x)$ para a onda quadrada,
$$2\times S_N(x) = \sin(x) + \frac{1}{3}\sin(3x) + \frac{1}{5}\sin(5x) + \dots + \frac{1}{N-1} \sin ((N-1)x),$$
onde o último termo só é não zero se $N$ for par.
Nós temos
$2\times S_N(\pi/N) = \sin(\pi/N) + \frac{1}{3}\sin(3\pi/N) + \frac{1}{5}\sin(5\pi/N) + \dots + \frac{1}{N} \sin ((N-1) \pi/N), $
$ =\times( 0 + \frac{\pi}{N}\frac{\sin(\frac{\pi}{N})}{\frac{\pi}{N}} + \frac{\pi}{N}\frac{\sin(\frac{3\pi}{N})}{\frac{3\pi}{N}} +
\frac{\pi}{N}\frac{\sin(\frac{5\pi}{N})}{\frac{5\pi}{N}} + \dots +
\frac{\pi}{N}\frac{\sin(\frac{(N-1)\pi}{N})}{\frac{\pi}{N}}).$
Tomando o limite $N \to \infty$ a soma parcial na última linha se torna,
$\to \int_0^{\pi} \frac{\sin(x)}{x} dx = 1.85194 \Rightarrow S_N(\pi/N) \approx 0.5 \times 1.85194 \approx \pi/4 + 0.08 \times \pi/2 . $
(Nós tínhamos uma soma de Riemann no intervalo de $[0,\pi]$, onde na aproximação por retângulos nós dividimos o intervalo em $k$ ou $k-1$ subintervalos, dependendo se $N=2k$ ou $2k-1$ e a altura de cada sub-retângulo era o valor da função no meio dos subintervalos.)
A função $\text{sinc}(x) = \sin(x)/x$ é bem conhecida na literatura, e é continua no intervalo $[0,\pi]$.
Lista de exercícios 2
Em análise nós provamos o seguinte.
Suponha que $f_n:[a,b]\to \mathbb{R}$ é contínua para cada $n$ e que $(f_n)$ converge uniformemente para cada $f$ em $[a,b]$. Então $\int_a^b f_n(x) dx \to \int_a^b f(x) dx$.
- Suponha que a série trigonométrica $a_0/2 + \sum^\infty_{n=1}(a_n \cos(nx) + b_n\sin(nx))$ é uniformemente convergente no intervalo $[-\pi,\pi]$. Seja $f(x)$ essa função limite. Prove que essa série coincide com a série de Fourier de $f(x)$.
- Mostre que para uma função contínua $2\pi$ periódica $f$, se $(f,\exp(ikx))=0$ ou equivalentemente $\int_{-\pi}^{\pi} f(x)\cos(kx) dx=\int_{-\pi}^{\pi} f(x)\sin(kx) dx = 0$ para todo $k$ então $f$ é necessariamente a função constante igual à zero.
- Prove que se a série de Fourier de uma função $f(x)$ for uniformemente convergente, então essa série funções converge para $f(x)$.
Dicas para o segundo problema.
A função $g(y) = f(\arccos y)$ define uma função contínua para $y\in [-1,1]$. Portanto pelo teorema de aproximação de Weiertrass existe um polinômio $p(y)$ tal que $\max_{\vert y\vert \leq 1}\vert f(\arccos(y)) - p(y)\vert < \epsilon.$ Mas $T(x) = p(\cos(x))$ é um polinômio trigonométrico, e portanto
$\max_{x\in [0,\pi]}\vert f(x) - p(\cos(x))\vert < \epsilon.$
Portanto toda função contínua, e periódica pode ser aproximada uniformemente por um polinômio trigonométrico.
Portanto pelo teorema de Weierstrass existe uma seqüência de polinômios trigonométricos $(p_n)$ que converge uniformemente para $f(x)$.
Mas já que tomar as operações de tomar o limite e integração comutem no caso de convergência uniforme nós temos que,
$\int_{-\pi}^{\pi}f^2(x)dx = \lim_{n\to \infty} \int_{-\pi}^{\pi}f(x) p_n(x) dx. $
Conclua a demonstração.
Dica para o terceiro problema. Combine os exercícios 1 e 3.
sexta-feira, 12 de agosto de 2011
Resumo da aula 3
Nós começamos por falar sobre como representar uma função periódica $\phi(x)$ de período $2\pi$ como uma série infinita (em geral), da forma
$\phi = a_0 + \sum_{k=1}^{\infty}(a_k \cos(kx) + b_k\sin(kx)),$ ou como
$\phi = \sum_{k=-\infty}^{\infty}c_k\exp(ikx). $
A igualdade aqui é formal, pois ainda não sabemos se a série de funções à direita converge ou não para a função na esquerda.
Dada uma função $\phi(x)$ o procedimento para obtermos uma série infinita foi através de ''projeções ortogonais''. Isso significa que
$\int_{-\pi}^{\pi} \phi(x) \exp(-ikx) dx = \dots + \int_{-\pi}^{\pi}c_{-2}\exp(-i2x) \exp(-ikx)dx + $
$ \int_{-\pi}^{\pi}c_{-1}\exp(-ix) \exp(-ikx)dx + \int_{-\pi}^{\pi}c_{0} \exp(ikx)dx +\int_{-\pi}^{\pi}c_{1} \exp(ix)\exp(-ikx)dx + \dots .$
Usando a relação $(\exp(ikx),\exp(ilx)) = \int_{-\pi}^{\pi} \exp(ikx)\exp(ilx) dx = 0$ se $k\neq l$,
então,
$$c_k =(\phi(x),\exp(ikx))/(\exp(ikx),\exp(ikx)). $$
Mas dada a série $ \sum_{k=-\infty}^{\infty}c_k\exp(ikx)$,
Se $\phi(x) \in C^2(S^1)$, i.e. $\phi(x)$ é $C^2$ e periódica de período $2\pi$, então os coeficientes em
$\sum c_k \exp(ikx)$ têm decaimento quadrático,
$$\vert c_k\vert < A/\vert k\vert^2,$$
onde a constante $A$ só depende de $\phi$.
Primeiramente, todos os $c_k$'s são limitados, $$\vert c_k\vert = \vert \int \phi(x)\exp(-ikx) dx\vert \leq
\int \vert \phi(x) \exp(ikx)\vert dx = \int \vert \phi(x)\vert dx = M.$$
Prova consiste de uma aplicação direta de integração por partes,
$c_k = \int_{\pi}^{\pi} \phi(x)\exp(ikx) dx = \frac{-1}{ik}\int_{\pi}^{\pi} \phi(x) d(\exp(-ikx)) $
$ = \frac{-1}{ik}\phi(x)\exp(-ikx) \vert_{x=-\pi}^{x=\pi} + \frac{-1}{k^2}\int_{\pi}^{\pi} \phi'(x) d(\exp(-ikx))$
$ = \frac{-1}{k^2}\phi'(x)\exp(-ikx) \vert_{x=-\pi}^{x=\pi} + \frac{1}{k^2}\int_{\pi}^{\pi} \phi''(x) \exp(-ikx) dx,$
e portanto
$\vert c_k\vert \leq \vert \frac{1}{k^2}\int_{\pi}^{\pi} \phi''(x) \exp(-ikx) dx\vert \leq \frac{A}{kˆ2}.$
(Ache a constante $A$.)
Agora nós invocaremos Herr Weierstrass duas vezes,
a primeira para provarmos a convergência da série de Fourier de $\phi(x)$ e na segunda vez nós utilizaremos um teorema de Weierstrass em teoria de aproximação.
Teorema. ( Teste de Weierstrass. ) A série de funções $\sum f_k(x)$ converge uniformemente se
$\phi = a_0 + \sum_{k=1}^{\infty}(a_k \cos(kx) + b_k\sin(kx)),$ ou como
$\phi = \sum_{k=-\infty}^{\infty}c_k\exp(ikx). $
A igualdade aqui é formal, pois ainda não sabemos se a série de funções à direita converge ou não para a função na esquerda.
Dada uma função $\phi(x)$ o procedimento para obtermos uma série infinita foi através de ''projeções ortogonais''. Isso significa que
$\int_{-\pi}^{\pi} \phi(x) \exp(-ikx) dx = \dots + \int_{-\pi}^{\pi}c_{-2}\exp(-i2x) \exp(-ikx)dx + $
$ \int_{-\pi}^{\pi}c_{-1}\exp(-ix) \exp(-ikx)dx + \int_{-\pi}^{\pi}c_{0} \exp(ikx)dx +\int_{-\pi}^{\pi}c_{1} \exp(ix)\exp(-ikx)dx + \dots .$
Usando a relação $(\exp(ikx),\exp(ilx)) = \int_{-\pi}^{\pi} \exp(ikx)\exp(ilx) dx = 0$ se $k\neq l$,
então,
$$c_k =(\phi(x),\exp(ikx))/(\exp(ikx),\exp(ikx)). $$
Mas dada a série $ \sum_{k=-\infty}^{\infty}c_k\exp(ikx)$,
- será que a série converge? E se ela converge,
- será que ela converge para a função original?
A resposta para a primeira pergunta depende do comportamento da função original. Vamos começar com o caso onde $\phi(x)$ é $C^2$. Isso foi motivado pelos nossos estudos da equação da corda e pela fórmula de D'Alembert.
Primeiro nós devemos mostrar o seguinte,
Proposição.
Se $\phi(x) \in C^2(S^1)$, i.e. $\phi(x)$ é $C^2$ e periódica de período $2\pi$, então os coeficientes em
$\sum c_k \exp(ikx)$ têm decaimento quadrático,
$$\vert c_k\vert < A/\vert k\vert^2,$$
onde a constante $A$ só depende de $\phi$.
Primeiramente, todos os $c_k$'s são limitados, $$\vert c_k\vert = \vert \int \phi(x)\exp(-ikx) dx\vert \leq
\int \vert \phi(x) \exp(ikx)\vert dx = \int \vert \phi(x)\vert dx = M.$$
Prova consiste de uma aplicação direta de integração por partes,
$c_k = \int_{\pi}^{\pi} \phi(x)\exp(ikx) dx = \frac{-1}{ik}\int_{\pi}^{\pi} \phi(x) d(\exp(-ikx)) $
$ = \frac{-1}{ik}\phi(x)\exp(-ikx) \vert_{x=-\pi}^{x=\pi} + \frac{-1}{k^2}\int_{\pi}^{\pi} \phi'(x) d(\exp(-ikx))$
$ = \frac{-1}{k^2}\phi'(x)\exp(-ikx) \vert_{x=-\pi}^{x=\pi} + \frac{1}{k^2}\int_{\pi}^{\pi} \phi''(x) \exp(-ikx) dx,$
e portanto
$\vert c_k\vert \leq \vert \frac{1}{k^2}\int_{\pi}^{\pi} \phi''(x) \exp(-ikx) dx\vert \leq \frac{A}{kˆ2}.$
(Ache a constante $A$.)
Agora nós invocaremos Herr Weierstrass duas vezes,
a primeira para provarmos a convergência da série de Fourier de $\phi(x)$ e na segunda vez nós utilizaremos um teorema de Weierstrass em teoria de aproximação.
Teorema. ( Teste de Weierstrass. ) A série de funções $\sum f_k(x)$ converge uniformemente se
- $\vert f_k \vert \leq M_k$,
- $\sum M_k < \infty$. (A série das quotas superiores converge.)
A prova pode ser encontrada em qualquer livro de análise clássica. (Cf. F. John e R. Courant, Intro. to Analysis and Calculus.)
Corolário. A série de Fourier de uma função $C^2$ converge uniformemente para alguma função.
Quem é essa função limite? Você adivinhou corretamente se o seu chute for $\phi(x)$. Mas a prova não é tão banal. Na postagem anterior eu inclui uma prova desse fato. Outro fato interessante é que se $\phi(x)$ é analítica, i.e. $\phi(x)$ é a restrição de alguma função holomórfica ao intervalo $[-\pi,\pi]$,
a convergência da série de Fourier é super-rápida já que os coeficientes decaem exponencialmente.
Por quê falávamos de séries de Fourier?
Nosso objetivo era resolver o problema de Cauchy,
$u_{tt} - a^2u_{xx} = 0, u\vert_{t=0} = \phi(x), u_t\vert_{t=0} = \psi(x),$$
e com condições de fronteira periódicas: $u(x+2\pi,t) = u(x,t)$.
Nós queremos provar que (supondo $a=1$)
$$u(x,t) = \sum_{k=-\infty}^{\infty} (a_k \cos(kt) + b_k \sin(kt)) \exp(ikx),$$
é solução geral do problema de fronteiras, e em seguida utilizamos as condições iniciais para determinarmos os coeficientes na série infinita acima.
Como exercício eu sugiro que você rescreva a o lado direito de $u(x,t)$ como
$\sum_{k=-\infty}^{\infty}(A_k e^{ik(t+x)} + B_k e^{ik(t-x)})$.
Cada um termos $e^{ik(t \pm x)}$ é chamado uma onda, movendo-se à direita ou à esquerda.
Verique que $e^{ik(t+x)}$ é solução da equação da onda.
Portanto a solução geral é uma superposição de ondas. Superposição é uma propriedade muito útil dos modelos lineares.
Antes de continuarmos com a teoria geral, vejamos alguns exemplos práticos e computacionais de séries de Fourier.
Nós vimos o exemplo da função,
onda quadrada =
$f(x) = x$ em $[-\pi,\pi]$ estendida periodicamente ao longo reta real.
$f(x) = x$ em $[-\pi,\pi]$ estendida periodicamente ao longo reta real.
Os coeficientes da série de Fourier dessa função foram calculados em classe.
Uma coisa intessante que está acontecendo na animação é a formação de um ruído nas extremidades do zig-zag.
Por quê?
Dica. A convergência não é uniforme.
Assinar:
Comentários (Atom)